Презентация - Свойства функции

Свойства функции
Токарева Инна Александровна учитель математики МБОУ гимназия №1 г. Липецка

Точки пересечения графика функции с осями координат. Монотонность функции (т.е. возрастание или убывание функции). Ограниченность функции. Наименьшее и наибольшее значение функции. Четность и нечетность функции. Выпуклость графика функции. Непрерывность функции.

1. Точки пересечения графика функции с осями координат.
Точка пересечения с осью Оу равна значению функции у(х) при х=0, т.е. у(0). Точки пересечения с осью Ох являются корнями уравнения у(х) = 0 и называются нулями функции.
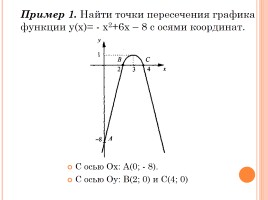
Пример 1. Найти точки пересечения графика функции у(х)= - х2+6х – 8 с осями координат.

С осью Ох: А(0; - 8). С осью Оу: В(2; 0) и С(4; 0)
Пример 1. Найти точки пересечения графика функции у(х)= - х2+6х – 8 с осями координат.

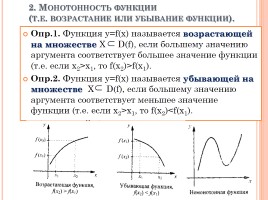
2. Монотонность функции (т.е. возрастание или убывание функции).
Опр.1. Функция у=f(х) называется возрастающей на множестве Х D(f), если большему значению аргумента соответствует большее значение функции (т.е. если х2>х1, то f(x2)>f(x1). Опр.2. Функция у=f(х) называется убывающей на множестве Х D(f), если большему значению аргумента соответствует меньшее значение функции (т.е. если х2>х1, то f(x2)

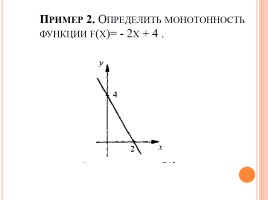
Пример 2. Определить монотонность функции f(x)= - 2x + 4 .

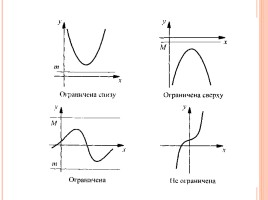
3. Ограниченность функции.
Опр.3. Функция у=f(х) называется ограниченной снизу на множестве Х D(f), если все значения функции больше некоторого числа m (т.е. f(x)>m). Опр.4. Функция у=f(х) называется ограниченной сверху на множестве Х D(f), если все значения функции меньше некоторого числа M (т.е. f(x)

Пример 3. Доказать, что функция f(х)= - х2+6х – 8 ограничена сверху.

Свойства функции

Точки пересечения графика функции с осями координат. Монотонность функции (т.е. возрастание или убывание функции). Ограниченность функции. Наименьшее и наибольшее значение функции. Четность и нечетность функции. Выпуклость графика функции. Непрерывность функции.

4. Наименьшее и наибольшее значение функции.
Опр.6. Число m называют наименьшим значением функции у=f(х) на множестве Х D(f), если: 1) существует число х0ϵ Х такое, что f(х0) = m; 2) для любого значения хϵ Х выполняется неравенство f(x)≥f(x0).
Опр.7. Число M называют наибольшим значением функции у=f(х) на множестве Х D(f), если: 1) существует число х0ϵ Х такое, что f(х0) = M; 2) для любого значения хϵ Х выполняется неравенство f(x)≤f(x0).

Пример 4. Найти наибольшее значение функции f(х)= - х2+6х – 8
Пример 5. Найти наименьшее и наибольшее значение функции f(х)= - 2х+4 на отрезке [-1;3]

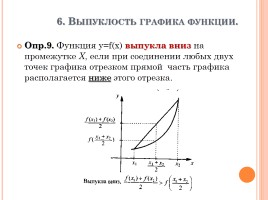
6. Выпуклость графика функции.
Опр.9. Функция у=f(х) выпукла вниз на промежутке Х, если при соединении любых двух точек графика отрезком прямой часть графика располагается ниже этого отрезка.

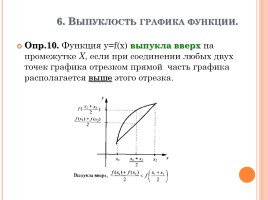
6. Выпуклость графика функции.
Опр.10. Функция у=f(х) выпукла вверх на промежутке Х, если при соединении любых двух точек графика отрезком прямой часть графика располагается выше этого отрезка.

7. Непрерывность функции.
Опр.11. Функция у=f(х) непрерывна на промежутке Х, если при малом изменении аргумента функция меняется незначительно. При этом график непрерывной функции сплошной и не имеет разрывов.

Схема исследования
1) область определения функции; 2) монотонность; 3) ограниченность; 4) унаим, унаиб; 5) непрерывность; 6) область значений; 7) выпуклость.
8) четность.

Четность и нечетность функции
Токарева Инна Александровна учитель математики МБОУ гимназия №1 г. Липецка

5. Четность и нечетность функции.
Область определения называется симметричной, если функция определена и в точке х0 и в точке ( - х0) (т.е. в точке симметричной х0 относительно начала числовой оси).
Пример 6. Найти область определения функции: а) б)

5. Четность и нечетность функции.
Понятие четности вводится только для функции с симметричной областью определения.
Опр.8. Функция называется четной, если при изменении знака аргумента значение функции не меняется, т.е. f(– x) = f(x).
Опр.9. Функция называется нечетной, если при изменении знака аргумента значение функции также меняется на противоположное, т.е. f(– x) = – f(x).

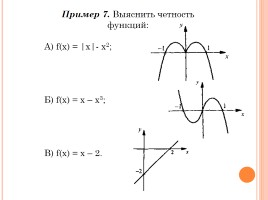
Пример 7. Выяснить четность функций: А) f(x) = |x|- x2; Б) f(x) = x – x3; В) f(х) = х – 2.