Презентация - Функция у = ах² и ее свойства

Функция у=ах2 и ее свойства.
Учитель МБОУ СОШ №67 г.Воронежа Кожеурова Галина Владимировна

Цели:
ввести понятие квадратичной функции; научится строить график функции у=ах2 и описывать свойства данной функции по графику; установить закономерность между графиком функции у=ах2 и значением коэффициента а.

Определение. Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2+bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем а≠0.

Из приведенных примеров укажите те функции, которые являются квадратичными. Для квадратичных функций назовите коэффициенты.

Функция у=ах2, ее график и свойства.

Построим графики функций
и исследуем их свойства.
1)
х -3 -2 -1 0 1 2 3
у
9
4
1
0
1
4
9

Построим графики функций
и исследуем их свойства.
1)
х -3 -2 -1 0 1 2 3
у
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если х=0
3. у>0, если х

Построим графики функций
и исследуем их свойства.
1)
х -3 -2 -1 0 1 2 3
у
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если х=0
3. у>0, если х
4. у↓, если х
у↑, если х

Построим графики функций
и исследуем их свойства.
1)
х -3 -2 -1 0 1 2 3
у
9
4
1
0
1
4
9
1. D(y): R
2. у=0, если х=0
3. у>0, если х
4. у↓, если х
у↑, если х
5. унаим=0, если х=0
унаиб – не существует.
6. Е(y):

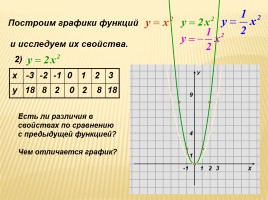
Построим графики функций
и исследуем их свойства.
2)
х -3 -2 -1 0 1 2 3
у
18
8
2
0
2
8
18
Есть ли различия в свойствах по сравнению с предыдущей функцией? Чем отличается график?

График функции у=kx2 может быть получен из графика функции у=x2 путем растяжения его вдоль оси Оу в k раз (k-натуральное число).

ФИЗМИНУТКА А теперь, ребята, встать Руки медленно поднять, Пальцы сжать, потом разжать, Руки вниз и так стоять. Наклонитесь вправо, влево. И беритесь вновь за дело.

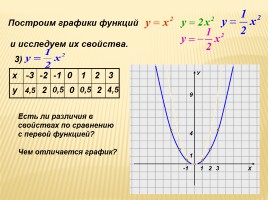
Построим графики функций
и исследуем их свойства.
3)
х -3 -2 -1 0 1 2 3
у
4,5
2
0,5
0
0,5
2
4,5
Есть ли различия в свойствах по сравнению с первой функцией? Чем отличается график?

График функции у= x2 может быть получен из графика функции у=x2 путем сжатия его вдоль оси Оу в k раз (k-натуральное число).

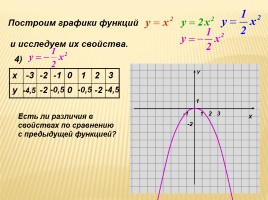
Построим графики функций
и исследуем их свойства.
4)
х -3 -2 -1 0 1 2 3
у
-4,5
-2
-0,5
0
-0,5
-2
-4,5
Есть ли различия в свойствах по сравнению с предыдущей функцией?

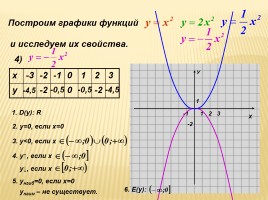
Построим графики функций
и исследуем их свойства.
4)
х -3 -2 -1 0 1 2 3
у
-4,5
-2
-0,5
0
-0,5
-2
-4,5
1. D(y): R
2. у=0, если х=0
3. у<0, если х
4. у↑, если х
у↓, если х
5. унаиб=0, если х=0
унаим – не существует.
6. Е(y):

График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох. Если а>0, то ветви параболы направлены… Если а<0, то ветви параболы направлены…

У
У
У
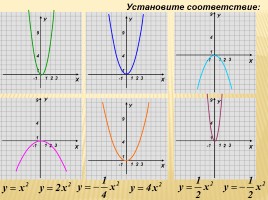
Установите соответствие: