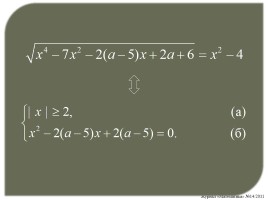Презентация - Различные способы решения задач с параметрами

РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ
11 класс

Задача 1
Найдите все значения параметра а, при которых уравнение имеет хотя бы один корень.

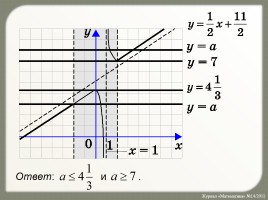
График левой части уравнения y = a — прямая, параллельная оси Ox. Построим график правой части уравнения:
 

3. Найдем производную: и ее экстремумы: y´ = 0 при x = 0, x = 2.

4. Найдем критические точки функции: ymax = y(0) = 5, ymin = y(2) = 7. 5. Найдем асимптоты: x = 1 — вертикальная асимптота;   — наклонная асимптота ( ).

6. Найдем значения функции в точках ±2: f(2) = 7, Отметим ограничение, данное в системе: полосу от –2 до 2, включая границы.

Ответ: и .

Задача 2
Найдите значения параметра а, при которых уравнение не имеет решения.

Условие (а) не выполняется при x (–2; 2). Условие (б) не выполняется в двух случаях: 1) уравнение (б) не имеет корней, то есть D < 0: (a – 5)2 – 2(a – 5) < 0 a (5; 7); (*)

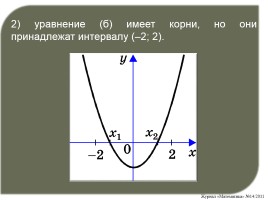
2) уравнение (б) имеет корни, но они принадлежат интервалу (–2; 2).

(**)

Объединяя множества (*) и (**), получаем: Итак, если , то уравнение не имеет решений, значит, при всех других значениях параметра a решения есть. Ответ: и .

Указания. Возможные способы решения: — используя теорему равносильности; — используя замену переменной; — графический способ; — ваши варианты.
Задача 3
Найдите значения параметра а, при каждом из которых уравнение имеет только одно решение.

Используем теорему равносильности

Чтобы исходное уравнение имело ровно один корень, надо потребовать, чтобы получившееся квадратное уравнение имело:
1-й случай
2-й случай
один корень, для которого выполнено условие
 

 
1-й случай

2-й случай
Рассмотрим случай, когда квадратное уравнение имеет два корня, то есть D > 0: 5 – 4a > 0 ⇔ a < 1,25;


x– < – a ≤ x+,

Рассмотрим неравенство
при всех a < 1,25.
Û
⇔ ⇔ 5 – 4a > 1 ⇔ a < 1.
 

Используем замену переменной
Исходное уравнение имеет один корень при тех и только тех значениях а, при которых полученное уравнение имеет один неотрицательный корень.
Пусть t ≥ 0, x = t2 – 1. Получим уравнение t2 – t – 1 + а = 0. (*)

Если D = 0, a = 1,25, то есть t = 0,5 > 0. Значит, исходное уравнение при а = 1,25 имеет один корень.
1
2
Если D > 0, то есть a < 1,25, уравнение (*) имеет два корня. При этом если a – 1 < 0, то эти корни разных знаков, то есть только один из них положительный.
При а < 1 уравнение (*) имеет один положительный корень, значит и исходное уравнение имеет один корень.
Ответ: a < 1, a = 1,25.

Графический способ I
Преобразуем уравнение к виду
Построим график функции, стоящей в левой части уравнения:

Алгоритм. 1. Найдем область определения функции. 2. Найдем точки пересечения с осями координат. 3. Найдем производную, критические точки и экстремумы функции.
ymax = y(–0,75) = 1,25

Ответ: a < 1, a = 1,25.

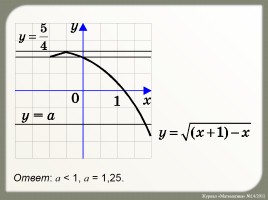
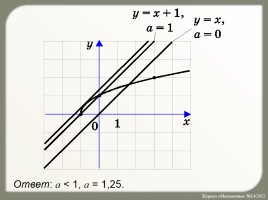
Графический способ II
Построим график левой и правой частей уравнения:
y = x + a.

Ответ: a < 1, a = 1,25.