Презентация - Алгоритм - Свойства алгоритма
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 99%
- Слайдов: 51
- Просмотров: 2683
- Скачиваний: 993
- Размер: 3.72 MB
- Класс: 9
- Формат: ppt / pptx
Примеры похожих презентаций
 Кибернетическая модель управления. Понятие алгоритма и его свойства
Кибернетическая модель управления. Понятие алгоритма и его свойства Алгоритм. Свойства алгоритма
Алгоритм. Свойства алгоритма Алгоритм. Свойства. Способы записи. Линейные алгоритмы.
Алгоритм. Свойства. Способы записи. Линейные алгоритмы. Алгоритм его виды и свойства
Алгоритм его виды и свойства Определение и свойства алгоритма
Определение и свойства алгоритма Знакомство с алгоритмом решения задач
Знакомство с алгоритмом решения задач Общий алгоритм работы образовательной организации с обучающимися с самоповреждающим и суицидальным поведением
Общий алгоритм работы образовательной организации с обучающимися с самоповреждающим и суицидальным поведением
Слайды и текст этой онлайн презентации
Слайд 1

К учебнику «Информатика и ИКТ» для 9 класса
© Н. Д. Угринович, 2009,
© БИНОМ. Лаборатория знаний, 2009
Основы алгоритмизации и объектно-ориентированного программирования
Основы алгоритмизации и объектно-ориентированного программирования
Слайд 2

Основы алгоритмизации
Урок №1. Алгоритм. Свойства алгоритма. Урок №2. Блок – схемы. Линейные алгоритмы, ветвление. Урок №3* Урок одной задачи – поиск НОД двух чисел. Урок №4. Алгоритмическая структура «цикл».
Урок №1. Алгоритм. Свойства алгоритма. Урок №2. Блок – схемы. Линейные алгоритмы, ветвление. Урок №3* Урок одной задачи – поиск НОД двух чисел. Урок №4. Алгоритмическая структура «цикл».
Слайд 3

Урок №1
Алгоритм. Свойства алгоритма.
Алгоритм. Свойства алгоритма.
Слайд 4

Повседневные задачи
" Мы редко до конца понимаем, чего мы в действительности хотим" Франсуа де Ларошфуко
Приготовление завтрака 2. Решение квадратного уравнения 3. Определение рода существительного
" Мы редко до конца понимаем, чего мы в действительности хотим" Франсуа де Ларошфуко
Приготовление завтрака 2. Решение квадратного уравнения 3. Определение рода существительного
Слайд 5

Определение 1
Алгоритм – это предписание исполнителю выполнить последовательность команд, приводящую от исходных данных к искомому результату.
Алгоритм – это предписание исполнителю выполнить последовательность команд, приводящую от исходных данных к искомому результату.
Слайд 6

Первый алгоритм
ЕВКЛИД (расцвет деятельности около 300 до н.э.), также Эвклид, древнегреческий математик, известный прежде всего как автор «Начал», самого знаменитого учебника в истории.
ЕВКЛИД (расцвет деятельности около 300 до н.э.), также Эвклид, древнегреческий математик, известный прежде всего как автор «Начал», самого знаменитого учебника в истории.
Слайд 7

Происхождение слова «алгоритм»
В IX веке жил Ал-Хорезми — сын зороастрийского жреца, прозванный за это ал-Маджуси (маг). Заведовал библиотекой «Дома мудрости», изучал индийские и греческие знания. Ал-Хорезми написал книгу «Об индийском счёте», способствовавшую популяризации позиционной системы во всём Халифате, вплоть до Испании. В XII веке эта книга переводится на латинский, от имени её автора происходит наше слово «алгоритм»
В IX веке жил Ал-Хорезми — сын зороастрийского жреца, прозванный за это ал-Маджуси (маг). Заведовал библиотекой «Дома мудрости», изучал индийские и греческие знания. Ал-Хорезми написал книгу «Об индийском счёте», способствовавшую популяризации позиционной системы во всём Халифате, вплоть до Испании. В XII веке эта книга переводится на латинский, от имени её автора происходит наше слово «алгоритм»
Слайд 8

Верно ли, что…
Налить воду в чайник Открыть кран газовой горелки Поставить чайник на плиту Ждать, пока вода не закипит Поднести спичку к горелке Зажечь спичку Выключить газ
Налить воду в чайник Открыть кран газовой горелки Поставить чайник на плиту Ждать, пока вода не закипит Поднести спичку к горелке Зажечь спичку Выключить газ
Слайд 9

Верно, что…
Налить воду в чайник Поставить чайник на плиту Зажечь спичку Открыть кран газовой горелки Поднести спичку к горелке Ждать, пока вода не закипит Выключить газ
Налить воду в чайник Поставить чайник на плиту Зажечь спичку Открыть кран газовой горелки Поднести спичку к горелке Ждать, пока вода не закипит Выключить газ
Слайд 10

Свойства алгоритма
дискретность: состоит из отдельных шагов (команд) результативность: применение алгоритма обязательно приводит к конечному результату за конечное число шагов массовость: может применяться многократно при различных исходных данных детерминированность: выполнение команд в строго определенной последовательности понятность: должен включать только команды, известные исполнителю (входящие в СКИ) определенность: при одинаковых исходных данных всегда выдает один и тот же результат корректность: дает верное решение при любых допустимых исходных данных
дискретность: состоит из отдельных шагов (команд) результативность: применение алгоритма обязательно приводит к конечному результату за конечное число шагов массовость: может применяться многократно при различных исходных данных детерминированность: выполнение команд в строго определенной последовательности понятность: должен включать только команды, известные исполнителю (входящие в СКИ) определенность: при одинаковых исходных данных всегда выдает один и тот же результат корректность: дает верное решение при любых допустимых исходных данных
Слайд 11

Определение 2
Алгоритм – это конечная последовательность указаний, адресованных исполнителю, четко и однозначно задающая процесс решения задач какого-либо типа во всех деталях и позволяющая получить за конечное число шагов результат, однозначно определяемый исходными данными.
Алгоритм – это конечная последовательность указаний, адресованных исполнителю, четко и однозначно задающая процесс решения задач какого-либо типа во всех деталях и позволяющая получить за конечное число шагов результат, однозначно определяемый исходными данными.
Слайд 12

Задача 1
Старик должен переправить на лодке через реку волка, козу и капусту. Лодка может выдержать только старика и одного “пассажира”. В каком порядке старик перевезет пассажиров? Не забудь, что волк может съесть козу, а коза – капусту. Найди 2 варианта решения.
Старик должен переправить на лодке через реку волка, козу и капусту. Лодка может выдержать только старика и одного “пассажира”. В каком порядке старик перевезет пассажиров? Не забудь, что волк может съесть козу, а коза – капусту. Найди 2 варианта решения.
Слайд 13
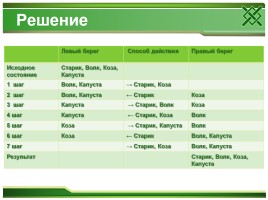
Решение
Слайд 14

Исполнитель алгоритма
Исполнитель алгоритма – это человек, животное или устройство способные выполнять определенный набор команд. Набор команд – СКИ (Система Команд Исполнителя). Алгоритм составляют с ориентацией на определенного исполнителя:
…формального или неформального?
Исполнитель алгоритма – это человек, животное или устройство способные выполнять определенный набор команд. Набор команд – СКИ (Система Команд Исполнителя). Алгоритм составляют с ориентацией на определенного исполнителя:
…формального или неформального?
Слайд 15

Задача №2
Выполните предложенные действия. Задумайте целое число от 1 до 20. Прибавьте к нему 2. Результат умножьте на 2. К полученному произведению прибавьте 3. От суммы отнимите задуманное число. К разности прибавьте 5. От суммы отнимите задуманное число. Сообщите ответ. Ответ: 12; мы выступали в роли формального исполнителя
Выполните предложенные действия. Задумайте целое число от 1 до 20. Прибавьте к нему 2. Результат умножьте на 2. К полученному произведению прибавьте 3. От суммы отнимите задуманное число. К разности прибавьте 5. От суммы отнимите задуманное число. Сообщите ответ. Ответ: 12; мы выступали в роли формального исполнителя
Слайд 16

Задача №3
Какому исполнителю под силу решить такую задачу: «Отгадай пословицу, обойдя поле ходом шахматного коня»?
Ответ: Не игла шьёт, а руки
A B C D E F G H
1 2345678
Неформальный исполнитель
Какому исполнителю под силу решить такую задачу: «Отгадай пословицу, обойдя поле ходом шахматного коня»?
Ответ: Не игла шьёт, а руки
A B C D E F G H
1 2345678
Неформальный исполнитель
Слайд 17

Задача №4*
Имеется Исполнитель алгоритма, который может передвигаться по числовой оси. Система команд Исполнителя алгоритма: «Вперед N» «Назад M» Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?
Имеется Исполнитель алгоритма, который может передвигаться по числовой оси. Система команд Исполнителя алгоритма: «Вперед N» «Назад M» Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?
Слайд 18

Решение:
1. Найдем сколько было команд: пусть х – количество команд «Вперед», тогда х+(х+12)=50; х=19; 19+12=31 – количество команд «Назад» 2. Будем вести отсчет от начала числовой оси: 19*3=57 – после выполнения «Вперед 3» 19 раз; 31*2=62 – после выполнения «Назад 2» 31 раз; 57-62=-5 – оказался на отметке -5. 3. Все эти команды можно заменить одной – «Назад 5»
1. Найдем сколько было команд: пусть х – количество команд «Вперед», тогда х+(х+12)=50; х=19; 19+12=31 – количество команд «Назад» 2. Будем вести отсчет от начала числовой оси: 19*3=57 – после выполнения «Вперед 3» 19 раз; 31*2=62 – после выполнения «Назад 2» 31 раз; 57-62=-5 – оказался на отметке -5. 3. Все эти команды можно заменить одной – «Назад 5»
Слайд 19

Задача №5**
Леонардо Пизанский, известный, как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который назван его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака»(1202 год). Он выглядит так: 1,1,2,3,5,8,13,21,34,55,89,144…
В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составьте словесный алгоритм проверки принадлежности введенного числа n ряду Фибоначчи.
Леонардо Пизанский, известный, как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который назван его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака»(1202 год). Он выглядит так: 1,1,2,3,5,8,13,21,34,55,89,144…
В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составьте словесный алгоритм проверки принадлежности введенного числа n ряду Фибоначчи.
Слайд 20

Решение:
1. Ввести число N. 2. Установить значение первых трех чисел Фибоначчи: 1,1,2. 3. Пока введенное число N больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи. 3. Если число Фибоначчи равно введенному N или было введено число N=1, значит, что было введено число Фибоначчи, в противном случае – введенное число не является числом Фибоначчи.
1. Ввести число N. 2. Установить значение первых трех чисел Фибоначчи: 1,1,2. 3. Пока введенное число N больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи. 3. Если число Фибоначчи равно введенному N или было введено число N=1, значит, что было введено число Фибоначчи, в противном случае – введенное число не является числом Фибоначчи.
Слайд 21

Способы записи алгоритмов
Словесный – на естественном языке; На языке блок – схем; На языке программирования.
Блок-схема – это графическое изображение алгоритма в виде определенным образом связанных между собой нескольких типов блоков.
Язык программирования — формальная знаковая система, предназначенная для записи компьютерных программ.
Словесный – на естественном языке; На языке блок – схем; На языке программирования.
Блок-схема – это графическое изображение алгоритма в виде определенным образом связанных между собой нескольких типов блоков.
Язык программирования — формальная знаковая система, предназначенная для записи компьютерных программ.
Слайд 22

Урок №2
Блок- схемы алгоритмов.
Блок- схемы алгоритмов.
Слайд 23
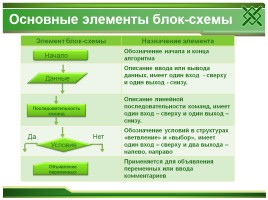
Основные элементы блок-схемы
Начало
Данные
Последовательность команд
Условие
Да
Нет
Объявление переменных
Начало
Данные
Последовательность команд
Условие
Да
Нет
Объявление переменных
Слайд 24

Линейный алгоритм
Линейный алгоритм – это набор команд, выполняемых последовательно во времени, друг за другом.
Линейный алгоритм – это набор команд, выполняемых последовательно во времени, друг за другом.
Слайд 25
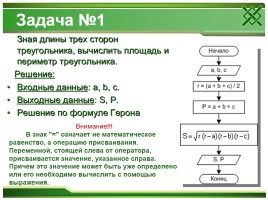
Задача №1
Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника. Решение: Входные данные: a, b, c. Выходные данные: S, P. Решение по формуле Герона
Внимание!!! В знак "=" означает не математическое равенство, а операцию присваивания. Переменной, стоящей слева от оператора, присваивается значение, указанное справа. Причем это значение может быть уже определено или его необходимо вычислить с помощью выражения.
Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника. Решение: Входные данные: a, b, c. Выходные данные: S, P. Решение по формуле Герона
Внимание!!! В знак "=" означает не математическое равенство, а операцию присваивания. Переменной, стоящей слева от оператора, присваивается значение, указанное справа. Причем это значение может быть уже определено или его необходимо вычислить с помощью выражения.
Слайд 26

Задача №2
Придумайте текст задачи, воспользовавшись предложенным алгоритмом, назовите входные и выходные данные:
Решение: Известны плотность и геометрические размеры цилиндрического слитка, полученного в металлургической лаборатории. Найти объем, массу и площадь основания слитка. Входные данные: R - радиус основания цилиндра, h - высота цилиндра, ρ- плотность материала слитка. Выходные данные: m - масса слитка, V - объем, S - площадь основания.
Придумайте текст задачи, воспользовавшись предложенным алгоритмом, назовите входные и выходные данные:
Решение: Известны плотность и геометрические размеры цилиндрического слитка, полученного в металлургической лаборатории. Найти объем, массу и площадь основания слитка. Входные данные: R - радиус основания цилиндра, h - высота цилиндра, ρ- плотность материала слитка. Выходные данные: m - масса слитка, V - объем, S - площадь основания.
Слайд 27
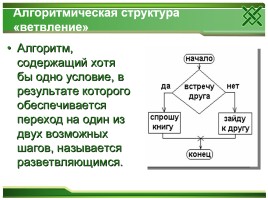
Алгоритмическая структура «ветвление»
Алгоритм, содержащий хотя бы одно условие, в результате которого обеспечивается переход на один из двух возможных шагов, называется разветвляющимся.
Алгоритм, содержащий хотя бы одно условие, в результате которого обеспечивается переход на один из двух возможных шагов, называется разветвляющимся.
Слайд 28
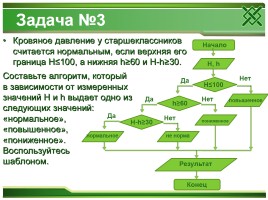
Задача №3
Кровяное давление у старшеклассников считается нормальным, если верхняя его граница H≤100, а нижняя h≥60 и H-h≥30.
Составьте алгоритм, который в зависимости от измеренных значений H и h выдает одно из следующих значений: «нормальное», «повышенное», «пониженное». Воспользуйтесь шаблоном.
Начало
H, h
H≤100
Нет
Нет
Нет
повышенное
Да
Да
Да
h≥60
пониженное
H-h≥30
не норма
нормальное
Результат
Конец
Кровяное давление у старшеклассников считается нормальным, если верхняя его граница H≤100, а нижняя h≥60 и H-h≥30.
Составьте алгоритм, который в зависимости от измеренных значений H и h выдает одно из следующих значений: «нормальное», «повышенное», «пониженное». Воспользуйтесь шаблоном.
Начало
H, h
H≤100
Нет
Нет
Нет
повышенное
Да
Да
Да
h≥60
пониженное
H-h≥30
не норма
нормальное
Результат
Конец
Слайд 29
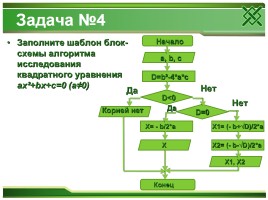
Задача №4
Заполните шаблон блок-схемы алгоритма исследования квадратного уравнения ax²+bx+c=0 (a≠0)
Начало
a, b, c
D=b²-4*a*c
D<0
Нет
Нет
Да
Корней нет
D=0
Да
Х= - b/2*a
Х
X1= (- b+√D)/2*a
X2= (- b-√D)/2*a
X1, X2
Конец
Заполните шаблон блок-схемы алгоритма исследования квадратного уравнения ax²+bx+c=0 (a≠0)
Начало
a, b, c
D=b²-4*a*c
D<0
Нет
Нет
Да
Корней нет
D=0
Да
Х= - b/2*a
Х
X1= (- b+√D)/2*a
X2= (- b-√D)/2*a
X1, X2
Конец
Слайд 30
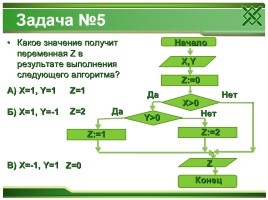
Задача №5
Какое значение получит переменная Z в результате выполнения следующего алгоритма?
Начало
X,Y
Z:=0
X>0
Y>0
Z:=1
Z:=2
Z
Конец
А) Х=1, Y=1 Б) X=1, Y=-1 В) X=-1, Y=1
Z=1
Z=2
Z=0
Нет
Нет
Да
Да
Какое значение получит переменная Z в результате выполнения следующего алгоритма?
Начало
X,Y
Z:=0
X>0
Y>0
Z:=1
Z:=2
Z
Конец
А) Х=1, Y=1 Б) X=1, Y=-1 В) X=-1, Y=1
Z=1
Z=2
Z=0
Нет
Нет
Да
Да
Слайд 31

Урок №3
Урок одной задачи. Поиск НОД двух чисел.*
Урок одной задачи. Поиск НОД двух чисел.*
Слайд 32

Первый алгоритм
Как-то раз древнегреческого геометра Евклида спросили: - Что бы ты предпочел - два целых яблока или четыре половинки? - Конечно, четыре половинки. - А почему? Это ведь одно и то же. - Отнюдь. Выбирая два целых яблока, как я узнаю, червивые они или нет?
Алгоритм Евклида – это алгоритм нахождения НОД двух целых положительных чисел
Как-то раз древнегреческого геометра Евклида спросили: - Что бы ты предпочел - два целых яблока или четыре половинки? - Конечно, четыре половинки. - А почему? Это ведь одно и то же. - Отнюдь. Выбирая два целых яблока, как я узнаю, червивые они или нет?
Алгоритм Евклида – это алгоритм нахождения НОД двух целых положительных чисел
Слайд 33

Методы решения:
1. Разложение на простые сомножители; 2. Алгоритм Евклида; 3. Целочисленное деление.
Существуют различные методы нахождения НОД двух натуральных чисел:
1. Разложение на простые сомножители; 2. Алгоритм Евклида; 3. Целочисленное деление.
Существуют различные методы нахождения НОД двух натуральных чисел:
Слайд 34

Разложение на простые множители
Порядок действий: 1. Разложить число m на простые множители. 2. Разложить число n на простые множители. 3. Выбрать все одинаковые множители чисел m и n. 4. Перемножить выбранные множители – полученное значение и будет НОД (m;n).
НОД (5390; 2310) = = 2*5*7*11=770;
Порядок действий: 1. Разложить число m на простые множители. 2. Разложить число n на простые множители. 3. Выбрать все одинаковые множители чисел m и n. 4. Перемножить выбранные множители – полученное значение и будет НОД (m;n).
НОД (5390; 2310) = = 2*5*7*11=770;
Слайд 35

Рекурсивный метод – алгоритм Евклида
В соответствии с этим методом НОД(m,n) вычисляется по следующему правилу:
НОД(m,n) =
НОД(m-n,n), если m>n, НОД(m,n-m), если n>m, m, если m=n.
т.е. если d является НОД(m,n), то это же число d будет являться НОД меньшего числа из этой пары и их разности.
В соответствии с этим методом НОД(m,n) вычисляется по следующему правилу:
НОД(m,n) =
НОД(m-n,n), если m>n, НОД(m,n-m), если n>m, m, если m=n.
т.е. если d является НОД(m,n), то это же число d будет являться НОД меньшего числа из этой пары и их разности.
Слайд 36
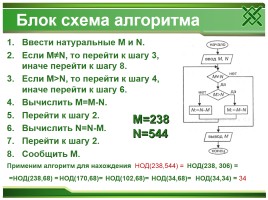
Блок схема алгоритма
Ввести натуральные M и N. Если M≠N, то перейти к шагу 3, иначе перейти к шагу 8. Если M>N, то перейти к шагу 4, иначе перейти к шагу 6. Вычислить M=M-N. Перейти к шагу 2. Вычислить N=N-M. Перейти к шагу 2. Сообщить M.
Применим алгоритм для нахождения НОД(238,544) =
НОД(238, 306) =
=НОД(238,68) =
НОД(170,68)=
НОД(102,68)=
НОД(34,68)=
НОД(34,34) = 34
M=238 N=544
Ввести натуральные M и N. Если M≠N, то перейти к шагу 3, иначе перейти к шагу 8. Если M>N, то перейти к шагу 4, иначе перейти к шагу 6. Вычислить M=M-N. Перейти к шагу 2. Вычислить N=N-M. Перейти к шагу 2. Сообщить M.
Применим алгоритм для нахождения НОД(238,544) =
НОД(238, 306) =
=НОД(238,68) =
НОД(170,68)=
НОД(102,68)=
НОД(34,68)=
НОД(34,34) = 34
M=238 N=544
Слайд 37

Метод целочисленного деления
Первое число делим нацело на второе. Очевидно, что остаток целочисленного деления меньше второго числа. Если остаток равен нулю, то это значит, что первое число нацело делится на второе, и в этом случае второе число и будем считать НОД этих чисел. Если остаток не равен нулю, то заменим первое число на второе, а второе - на остаток, и будем повторять действия до тех пор, пока остаток не станет равным нулю.
Первое число делим нацело на второе. Очевидно, что остаток целочисленного деления меньше второго числа. Если остаток равен нулю, то это значит, что первое число нацело делится на второе, и в этом случае второе число и будем считать НОД этих чисел. Если остаток не равен нулю, то заменим первое число на второе, а второе - на остаток, и будем повторять действия до тех пор, пока остаток не станет равным нулю.
Слайд 38
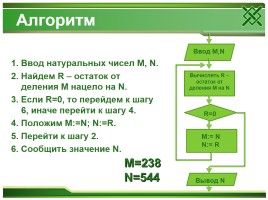
Алгоритм
1. Ввод натуральных чисел M, N. 2. Найдем R – остаток от деления M нацело на N. 3. Если R=0, то перейдем к шагу 6, иначе перейти к шагу 4. 4. Положим M:=N; N:=R. 5. Перейти к шагу 2. 6. Сообщить значение N.
Ввод M,N
Вычислить R – остаток от деления M на N
R=0
M:= N N:= R
Вывод N
M=238 N=544
1. Ввод натуральных чисел M, N. 2. Найдем R – остаток от деления M нацело на N. 3. Если R=0, то перейдем к шагу 6, иначе перейти к шагу 4. 4. Положим M:=N; N:=R. 5. Перейти к шагу 2. 6. Сообщить значение N.
Ввод M,N
Вычислить R – остаток от деления M на N
R=0
M:= N N:= R
Вывод N
M=238 N=544
Слайд 39

Пошаговое исполнение алгоритма
M:=238 N:=544 [238/544]=0 (ост. 238), заменяем: M:=544, N:=238 [544/238]=2 (ост. 68), заменяем: M:=238, N:=68 [238/68]=3 (ост. 34), заменяем: M:=68, N:=34 [68/34]=2 (ост. 0), закончили процесс деления. НОД(238, 544)=34
M:=238 N:=544 [238/544]=0 (ост. 238), заменяем: M:=544, N:=238 [544/238]=2 (ост. 68), заменяем: M:=238, N:=68 [238/68]=3 (ост. 34), заменяем: M:=68, N:=34 [68/34]=2 (ост. 0), закончили процесс деления. НОД(238, 544)=34
Слайд 40

Сравним количество операций
M=238,N=544
Почти одинаковое количество операций?
M=32000, N=2
M=238,N=544
Почти одинаковое количество операций?
M=32000, N=2
Слайд 41

Задание по группам:
По словесным описаниям методов поиска наибольшего из трех чисел постройте их блок-схемы и напишите пошаговый алгоритм. Метод 1: Даны три числа. Находим наибольшее из первых двух чисел, а затем сравниваем его с третьим числом. Метод 2: Определяем, является ли первое число наибольшим; если нет, то находим наибольшее из второго и третьего чисел. Метод 3: Попарно сравниваем все три числа, чтобы найти наибольшее.
По словесным описаниям методов поиска наибольшего из трех чисел постройте их блок-схемы и напишите пошаговый алгоритм. Метод 1: Даны три числа. Находим наибольшее из первых двух чисел, а затем сравниваем его с третьим числом. Метод 2: Определяем, является ли первое число наибольшим; если нет, то находим наибольшее из второго и третьего чисел. Метод 3: Попарно сравниваем все три числа, чтобы найти наибольшее.
Слайд 42

Урок №4
Алгоритмическая структура «цикл»
Алгоритмическая структура «цикл»
Слайд 43
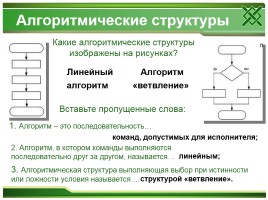
Алгоритмические структуры
Какие алгоритмические структуры изображены на рисунках?
Линейный алгоритм
Алгоритм «ветвление»
Вставьте пропущенные слова:
2. Алгоритм, в котором команды выполняются последовательно друг за другом, называется…
1. Алгоритм – это последовательность…
команд, допустимых для исполнителя;
линейным;
3. Алгоритмическая структура выполняющая выбор при истинности или ложности условия называется …
структурой «ветвление».
Какие алгоритмические структуры изображены на рисунках?
Линейный алгоритм
Алгоритм «ветвление»
Вставьте пропущенные слова:
2. Алгоритм, в котором команды выполняются последовательно друг за другом, называется…
1. Алгоритм – это последовательность…
команд, допустимых для исполнителя;
линейным;
3. Алгоритмическая структура выполняющая выбор при истинности или ложности условия называется …
структурой «ветвление».
Слайд 44

Задачи ГИА
№1. Какая алгоритмическая структура используется А.С. Пушкиным в следующих отрывках из его произведений?
«Уж небо осенью дышало, Уж реже солнышко блистало, Короче становился день, Лесов таинственная сень С печальным шумом обнажалась…»
«Приходите в половине двенадцатого. Ступайте прямо на лестницу. Коли вы найдете кого в передней, то спросите, дома ли графиня. Вам скажут нет, - делать нечего. Вы должны будете воротиться. Но, вероятно, вы не встретите никого… Из передней ступайте налево, идите все прямо до графининой спальни. В спальне за ширмами увидите две двери: справа в кабинет;… слева в коридор, и тут же узенькая витая лестница, она ведет в мою комнату.»
№1. Какая алгоритмическая структура используется А.С. Пушкиным в следующих отрывках из его произведений?
«Уж небо осенью дышало, Уж реже солнышко блистало, Короче становился день, Лесов таинственная сень С печальным шумом обнажалась…»
«Приходите в половине двенадцатого. Ступайте прямо на лестницу. Коли вы найдете кого в передней, то спросите, дома ли графиня. Вам скажут нет, - делать нечего. Вы должны будете воротиться. Но, вероятно, вы не встретите никого… Из передней ступайте налево, идите все прямо до графининой спальни. В спальне за ширмами увидите две двери: справа в кабинет;… слева в коридор, и тут же узенькая витая лестница, она ведет в мою комнату.»
Слайд 45
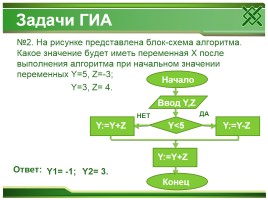
Задачи ГИА
№2. На рисунке представлена блок-схема алгоритма. Какое значение будет иметь переменная Х после выполнения алгоритма при начальном значении переменных Y=5, Z=-3; Y=3, Z= 4.
Начало
Ввод Y,Z
Y<5
ДА
НЕТ
Y:=Y+Z
Y:=Y-Z
Y:=Y+Z
Конец
Ответ:
Y1= -1;
Y2= 3.
№2. На рисунке представлена блок-схема алгоритма. Какое значение будет иметь переменная Х после выполнения алгоритма при начальном значении переменных Y=5, Z=-3; Y=3, Z= 4.
Начало
Ввод Y,Z
Y<5
ДА
НЕТ
Y:=Y+Z
Y:=Y-Z
Y:=Y+Z
Конец
Ответ:
Y1= -1;
Y2= 3.
Слайд 46
Игра «Ежиные тропы»
Слайд 47
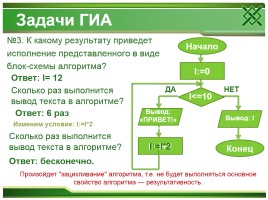
Задачи ГИА
№3. К какому результату приведет исполнение представленного в виде блок-схемы алгоритма?
Начало
I:=0
I<=10
НЕТ
ДА
Вывод: «ПРИВЕТ!»»
I:=I+2
Вывод: I
Конец
Ответ: I= 12
Сколько раз выполнится вывод текста в алгоритме?
Ответ: 6 раз
Изменим условие: I:=I*2
I:=I*2
Сколько раз выполнится вывод текста в алгоритме?
Ответ: бесконечно.
Произойдет "зацикливание" алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.
№3. К какому результату приведет исполнение представленного в виде блок-схемы алгоритма?
Начало
I:=0
I<=10
НЕТ
ДА
Вывод: «ПРИВЕТ!»»
I:=I+2
Вывод: I
Конец
Ответ: I= 12
Сколько раз выполнится вывод текста в алгоритме?
Ответ: 6 раз
Изменим условие: I:=I*2
I:=I*2
Сколько раз выполнится вывод текста в алгоритме?
Ответ: бесконечно.
Произойдет "зацикливание" алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.
Слайд 48
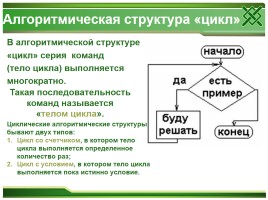
Алгоритмическая структура «цикл»
В алгоритмической структуре «цикл» серия команд (тело цикла) выполняется многократно.
Циклические алгоритмические структуры бывают двух типов: Цикл со счетчиком, в котором тело цикла выполняется определенное количество раз; Цикл с условием, в котором тело цикла выполняется пока истинно условие.
Такая последовательность команд называется «телом цикла».
В алгоритмической структуре «цикл» серия команд (тело цикла) выполняется многократно.
Циклические алгоритмические структуры бывают двух типов: Цикл со счетчиком, в котором тело цикла выполняется определенное количество раз; Цикл с условием, в котором тело цикла выполняется пока истинно условие.
Такая последовательность команд называется «телом цикла».
Слайд 49

Задачи ГИА
№3. Какая алгоритмическая структура используется А.С. Пушкиным в следующих отрывках из его произведений?
«Жил старик со своею старухой У самого синего моря; …
Вот пошел он к синему морю; Видит, — море слегка разыгралось. Стал он кликать золотую рыбку, Приплыла к нему рыбка и спросила: «Чего тебе надобно, старче?» …
Вот пошел он к синему морю, (Помутилося синее море.) Стал он кликать золотую рыбку, Приплыла к нему рыбка, спросила: «Чего тебе надобно, старче?»
№3. Какая алгоритмическая структура используется А.С. Пушкиным в следующих отрывках из его произведений?
«Жил старик со своею старухой У самого синего моря; …
Вот пошел он к синему морю; Видит, — море слегка разыгралось. Стал он кликать золотую рыбку, Приплыла к нему рыбка и спросила: «Чего тебе надобно, старче?» …
Вот пошел он к синему морю, (Помутилося синее море.) Стал он кликать золотую рыбку, Приплыла к нему рыбка, спросила: «Чего тебе надобно, старче?»
Слайд 50
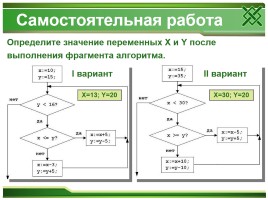
Самостоятельная работа
Определите значение переменных X и Y после выполнения фрагмента алгоритма.
I вариант
II вариант
Х=13; Y=20
Х=30; Y=20
Определите значение переменных X и Y после выполнения фрагмента алгоритма.
I вариант
II вариант
Х=13; Y=20
Х=30; Y=20
Слайд 51
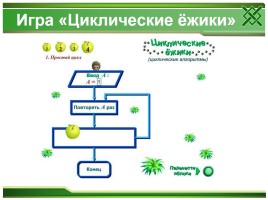
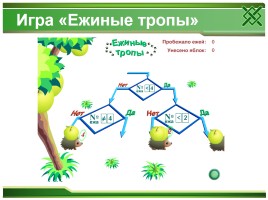
Игра «Циклические ёжики»
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
