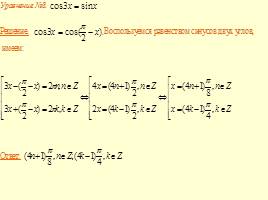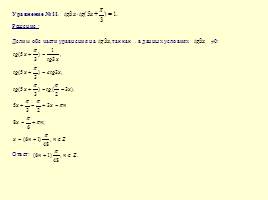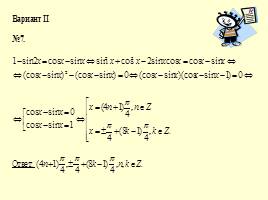Презентация - Методы решения тригонометрических уравнений

Методы решения тригонометрических уравнений
Выполнила: Маляренко Н.Д. МОУ «СОШ № 51 им. Ф.Д. Воронова» г.Магнитогорска

Уравнения.

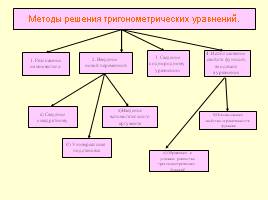
Методы решения тригонометрических уравнений.
1. Разложение на множители
2. Введение новой переменной
3. Сведение к однородному уравнению
4. Использование свойств функций, входящих в уравнение
а) Сведение к квадратному
б) Универсальная подстановка
в)Введение вспомогательного аргумента
а) Обращение к условию равенства тригонометрических функций
б)Использование свойства ограниченности функции

Классификация уравнений по методам.

Метод использования свойства ограниченности функции
Если функции f(x) и q(x) таковы, что для всех х выполняются неравенства f(x) ≤ a и q(x) ≤ b, и дано уравнение f(x)+q(x)=a+b, то оно равносильно системе f(x)=a, q(x)=b.

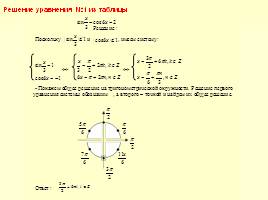
Решение уравнения №1 из таблицы

Условия равенства одноименных тригонометрических функций.

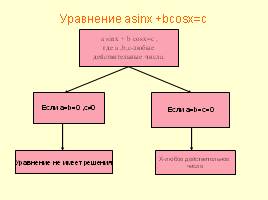
Уравнение asinx +bcosx=c
Если а=b=0 ,с≠0
Если а=b=с=0
а sinx + b cosx=c , где а ,b,с-любые действительные числа.
Х-любое действительное число
Уравнение не имеет решения

Шесть способов решения уравнения sin x+cos x =1

Ответ:

Самостоятельная работа

Ответ:

Домашнее задание: на «3» : решить уравнения из таблицы: №4 (любым способом), №5,№9. на «4» и «5» : решить уравнения из таблицы №2,№3,№4(несколькими способами).