Презентация - Логарифмическая функция, ее свойства и график
Примеры похожих презентаций
 Алгебра. Квадратичная функция. Функция. Функция у = kx², ее свойства и график
Алгебра. Квадратичная функция. Функция. Функция у = kx², ее свойства и график Урок алгебры по теме «Функция y=ax², её график и свойства» с применение системы учебных заданий как средства достижения планируемых результатов ФГОС. 9-й класс
Урок алгебры по теме «Функция y=ax², её график и свойства» с применение системы учебных заданий как средства достижения планируемых результатов ФГОС. 9-й класс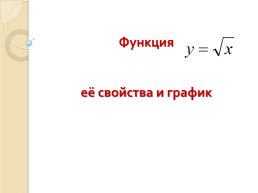 Функция её свойства и график
Функция её свойства и график … По улицам Архангельска. Линейная функция, её график и свойства
… По улицам Архангельска. Линейная функция, её график и свойства Свойства и графики Тригонометрических функций
Свойства и графики Тригонометрических функций Степенная функция с натуральным и целым показателем. Ее свойства и график
Степенная функция с натуральным и целым показателем. Ее свойства и график Квадратичная функция, ее график и свойства
Квадратичная функция, ее график и свойства
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.

