Презентация - Геометрия вокруг нас

Геометрия вокруг нас

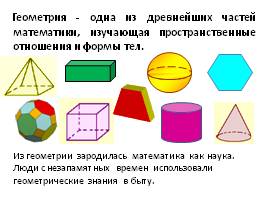
Геометрия - одна из древнейших частей математики, изучающая пространственные отношения и формы тел.
Из геометрии зародилась математика как наука. Люди с незапамятных времен использовали геометрические знания в быту.

Египетские пирамиды
Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей - Фараонов.

Пирамиды, а они построены более 5 тыс. лет назад, состоят из каменных блоков, весом 15 тонн и эти "кирпичики" так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы - рычаги и катки. "Все боится времени, но само время боится пирамид".
Египетские пирамиды

Вавилонская башня
В Вавилоне также при раскопках учёные обнаружили остатки каменных стен, высотой в несколько десятков метров. А сколько интересного связано с Вавилонской башней, высота её достигает 82 метров (восьмиэтажный дом).
Без математических знаний все эти сооружения невозможно было бы построить. Приглашаю вас заглянуть в различные уголки окружающего нас мира и посмотреть как там применяют геометрию.

Посмотри вокруг, и ты увидишь, что почти все предметы имеют форму: Апельсин и помидор похожи на шар; Клетка в зоопарке– на параллелепипед; Радуга - на дугу окружности. Простейшие геометрические фигуры, такие, как окружность, квадрат, трапеция и другие были известны людям в самые отдаленные времена.

ТРАПЕЦИЯ происходит от латинского слова «трапезиум» -столик. От этого же слова происходит наше слово « трапеза», означающее стол.
Трапеция

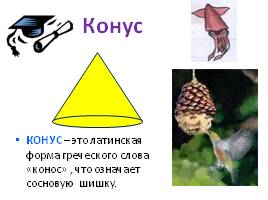
КОНУС – это латинская форма греческого слова «конос» , что означает сосновую шишку.
Конус

Конус
На токарном станке можно выточить конус. Цветочный горшок имеет форму перевернутого конуса с отрезанной нижней частью. Такую фигуру называют усеченным конусом.

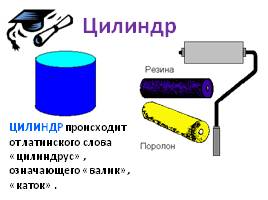
ЦИЛИНДР происходит от латинского слова «цилиндрус» , означающего «валик», «каток» .
Цилиндр

Цилиндр
Круглый карандаш, бревно, консервная банка имеют форму цилиндра. Цилиндрические предметы из металла или дерева вытачивают на токарном станке.

Пирамида – латинская форма греческого слова «пюрамис» , которым греки называли египетские пирамиды; это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне. Современные египтяне называют пирамиды словом «ахрам», которое также происходит от этого древнеегипетского слова .
Пирамида

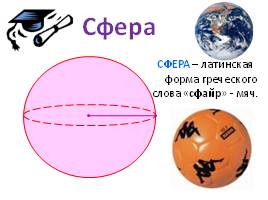
СФЕРА – латинская форма греческого слова «сфайр» - мяч.
Сфера

Окружность
Если поставить круглый стакан на лист бумаги и обвести его дно карандашом, получится линия, похожая на окружность. Многие вещи напоминают окружность — обруч, кольцо, дорожка вдоль арены цирка. Длину обруча или кольца можно вычислить по формуле С= 2πг, где π=3,14... . Орбиты планет, то есть линии, по которым они движутся вокруг Солнца,— это чуть-чуть сплюснутые окружности.

Круг
Окружность является границей круга. Арена цирка, дно стакана или тарелки имеют форму круга (по-латыни «циркус» и означает круг). Фигура, близкая к кругу, получится, если разрезать поперек арбуз.

Круг, шар
Со времени изобретения гончарного круга люди научились делать круглую посуду — горшки, вазы, амфоры. Круглыми были и колонны, подпиравшие здания. Среди круглых тел самым важным является шар. На геометрический шар похожи арбуз, глобус, футбольный мяч. Поэтому, когда у футбольных болельщиков до матча спрашивают, с каким счетом он кончится, они часто отвечают: «Не знаем — мяч круглый».

Шар
Из всех тел заданного объема шар имеет наименьшую площадь поверхности. Из-за этого на космическом корабле, находящемся в состоянии невесомости, пролитая вода собирается в водяной шар. Форму шара имеют и громадные сгустки материи — звезды и, в частности, Солнце. Но из-за вращения вокруг оси они немного сплюснуты. Земля тоже имеет форму немного сплюснутого шара (расстояние от центра Земли до полюса равно 6357 км, а до экватора — на 21 км больше). Но часто говорят «земной шар», пренебрегая сжатием Земли.

Прямоугольник
Многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Поверхности кирпича, спичечного коробка, куска мыла состоят из шести прямоугольных граней. Конечно, грани эти шероховаты, могут иметь выбоины или трещины, но с достаточной степенью точности можно вычислить их площади по формуле площади прямоугольника S=ab.

Прямоугольный параллелепипед
Комнаты, кирпичи, железобетонные блоки напоминают своей формой прямоугольный параллелепипед. Поэтому их объемы можно с хорошей точностью вычислять по формуле V=abc для объема прямоугольного параллелепипеда. Из одинаковых прямоугольных параллелепипедов можно сложить новое тело той же формы, но большего размера. Например, из кирпичей или железобетонных блоков складывают стены зданий.

Паркеты
Дощечки паркета, плитки, которыми покрывают полы в ванных комнатах и в метро, сверху ограничены многоугольниками.

Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
Треугольники

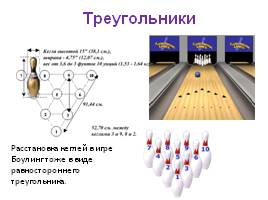
Расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника.
Треугольники

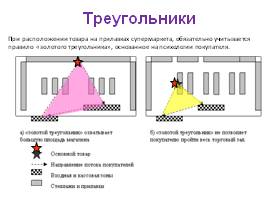
При расположении товара на прилавках супермаркета, обязательно учитывается правило «золотого треугольника», основанное на психологии покупателя.
Треугольники

Треугольники в конструкции мостов.

Высоковольтные линии электропередачи. Треугольники делают конструкции надежными.
Треугольники

Геометрия и архитектура
Геометрия - наука, давшая людям возможность находить площади и объемы, правильно чертить проекты зданий и машин. Она является основной частью «фундамента», на котором строится архитектура. Архитектура - это соединение искусства, науки и производства. Метко называют архитектуру дочерью геометрии.

Люди с древних времен, возводя свои жилища, думали, в первую очередь, об их прочности и долговечности. Благодаря этому, до наших дней дошли и древнегреческий Парфенон, и древнеримский Колизей. Прочность сооружения обеспечивается не только материалом, из которого оно создано, но и конструкцией, которая используется в качестве основы при его проектировании и строительстве. Прочность сооружения напрямую связана с той геометрической формой.

Пирамиды
Самым прочным архитектурным сооружением с давних времен считаются египетские пирамиды. Они имеют форму правильных четырехугольных пирамид. Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет большой площади основания. Форма пирамиды обеспечивает уменьшение массы по мере увеличения высоты над землей. Именно эти два свойства делают пирамиду устойчивой, а значит и прочной в условиях земного тяготения.

Стоечно-балочная конструкция
На смену пирамидам пришла стоечно-балочная система. она представляет собой многогранник, который получится, если мысленно на два вертикально стоящих прямоугольных параллелепипеда поставить еще один прямоугольный параллелепипед. Это одна из первых конструкций, которая представляет собой сооружения, состоящие из вертикальных стоек и покрывающих их горизонтальных балок. Первым таким сооружением было культовое сооружение – дольмен. Оно состояло из двух вертикально поставленных камней, на которые был поставлен третий вертикальный камень.

Стоечно-балочная конструкция
Кроме дольмена, до нас дошло еще одно сооружение, представляющее простейшую стоечно-балочную конструкцию – кромлех. Это культовое сооружение, предназначенное для жертвоприношений и ритуальных торжеств. Кромлех состоял из отдельно стоящих камней, которые накрывались горизонтальными камнями. При этом они образовывали две или несколько концентрических окружностей.

Стоечно-балочная конструкция
Самый знаменитый кромлех сохранился до наших дней в местечке Стоунхендж в Англии. Некоторые ученые считают, что он был древней астрономической обсерваторией.

Стоечно-балочная конструкция
Большинство современных жилых домов в своей основе имеют именно стоечно-балочную конструкцию.

С появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей, вошли окружности, круги, сферы и круговые цилиндры. Первоначально в архитектуре использовались только полуциркульные арки или полусферические купола.
Арочно-сводчатая конструкция

Пантеон
Полусферический купол имеет Пантеон – храм всех богов - в Риме. Диаметр купола составляет 43 м. При этом высота стен Пантеона равна радиусу полусферы купола. В связи с этим получается, что само здание этого храма как бы “накинуто” на шар диаметром 43 м.

Арочно-сводчатая конструкция
Арочно-сводчатая конструкция позволяла древнеримским архитекторам возводить гигантские сооружения из камня. К ним относится знаменитый Колизей или амфитеатр Флавиев. Свое название он получил от латинского слова colosseus, которое переводится как колоссальный, или огромный.

Каркасная конструкция
Арочная конструкция послужила прототипом каркасной конструкции, которая сегодня используется в качестве основной при возведении современных сооружений из металла, стекла и бетона. Достаточно вспомнить конструкции известных башен: Эйфелевой башни в Париже и телебашни на Шаболовке.

Телебашня на Шаболовке состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов. Причем каждая часть сделана из двух семейств прямолинейных балок. Эта башня построена по проекту замечательного инженера В.Г.Шухова
Каркасная конструкция
19 марта 2007 года Шуховской башне на Шаболовке исполнилось 85 лет.

Пентагон
Геометрическая форма сооружения настолько важна, что бывают случаи, когда в имени или названии здания закрепляются названия геометрических фигур. Так, здание военного ведомства США носит название Пентагон, что означает пятиугольник. Связано это с тем, что, если посмотреть на это здание с большой высоты, то оно действительно будет иметь вид пятиугольника. На самом деле только контуры этого здания представляют пятиугольник. Само же оно имеет форму многогранника.

Спасская башня
В Спасской башне Московского кремля в основании можно увидеть прямой параллелепипед, переходящий в средней части в фигуру, приближающуюся к цилиндру, завершается же она пирамидой. При более детальном рассмотрении и изучении деталей можно увидеть: круги – циферблаты курантов; шар – основание для крепления рубиновой звезды; полукруги – арки одного из рядов бойниц на фасаде башни и т.д.

Современный архитектурный стиль
Современный архитектурный стиль, благодаря возможностям современных материалов, использует причудливые формы, которые воспринимаются нами через их сложные, изогнутые (выпуклые и вогнутые) поверхности.

Современный архитектурный стиль

Современный архитектурный стиль
Таким образом, можно говорить о пространственных геометрических фигурах, которые служат основой сооружения в целом или отдельных его частей, а также плоских фигурах, которые обнаруживаются на фасадах зданий.

При постройке современных зданий, различных сооружений, технических устройств необходимы знания геометрии. Геометрия необходима рабочим многих специальностей, имеющим дело с обработкой дерева, металла. Посмотри на мир вокруг себя внимательно, и ты увидишь, что все связано с математикой, геометрией.