Презентация - Многогранники, описанные около сферы

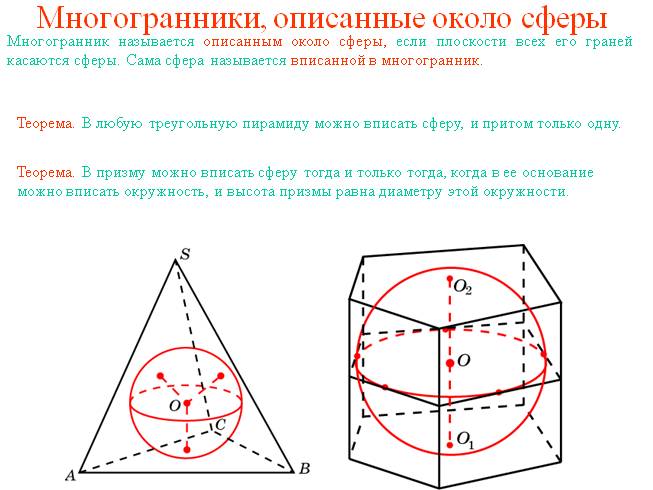
Многогранники, описанные около сферы
Многогранник называется описанным около сферы, если плоскости всех его граней касаются сферы. Сама сфера называется вписанной в многогранник.
Теорема. В призму можно вписать сферу тогда и только тогда, когда в ее основание можно вписать окружность, и высота призмы равна диаметру этой окружности.
Теорема. В любую треугольную пирамиду можно вписать сферу, и притом только одну.

Сфера, вписанная в куб

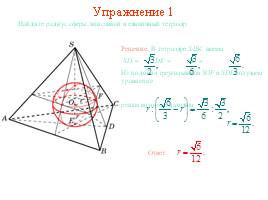
Упражнение 1
Найдите радиус сферы, вписанной в единичный куб.

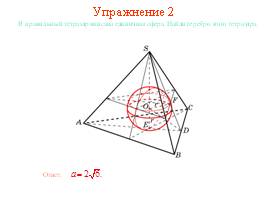
Упражнение 2
В куб вписана сфера радиуса 1. Найдите ребро куба.
Ответ: 2.

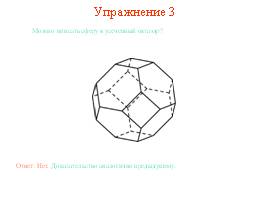
Упражнение 3
Можно ли вписать сферу в прямоугольный параллелепипед, отличный от куба?
Ответ: Нет.

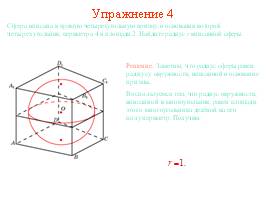
Упражнение 4
Можно ли вписать сферу в наклонный параллелепипед, все грани которого ромбы?
Ответ: Нет.

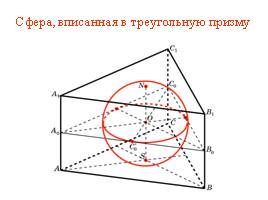
Сфера, вписанная в треугольную призму

Упражнение 1
Можно ли вписать сферу в наклонную треугольную призму, в основании которой правильный треугольник?
Ответ: Нет.

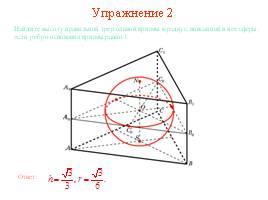
Упражнение 2
Найдите высоту правильной треугольной призмы и радиус, вписанной в нее сферы, если ребро основания призмы равно 1.

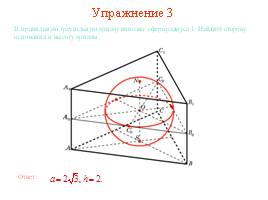
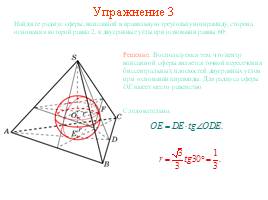
Упражнение 3
В правильную треугольную призму вписана сфера радиуса 1. Найдите сторону основания и высоту призмы.

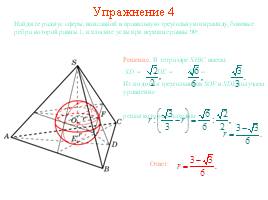
Упражнение 4
В призму, в основании которой прямоугольный треугольник с катетами, равными 1, вписана сфера. Найдите радиус сферы и высоту призмы.

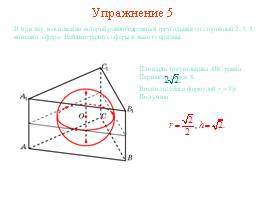
Упражнение 5
В призму, в основании которой равнобедренный треугольник со сторонами 2, 3, 3, вписана сфера. Найдите радиус сферы и высоту призмы.

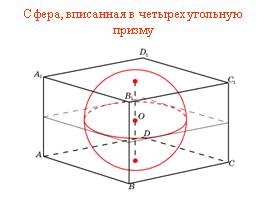
Сфера, вписанная в четырехугольную призму

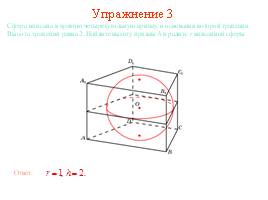
Упражнение 1
Сфера вписана в прямую четырехугольную призму, в основании которой ромб со стороной 1 и острым углом 60о. Найдите радиус сферы и высоту призмы.

Упражнение 2
Единичная сфера вписана в прямую четырехугольную призму, в основании которой ромб с острым углом 60о. Найдите сторону основания a и высоту призмы h.

Упражнение 3
Сфера вписана в прямую четырехугольную призму, в основании которой трапеция. Высота трапеции равна 2. Найдите высоту призмы h и радиус r вписанной сферы.

Упражнение 4
Сфера вписана в прямую четырехугольную призму, в основании которой четырехугольник, периметра 4 и площади 2. Найдите радиус r вписанной сферы.

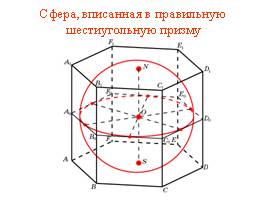
Сфера, вписанная в правильную шестиугольную призму

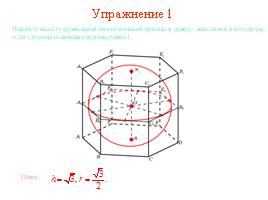
Упражнение 1
Найдите высоту правильной шестиугольной призмы и радиус, вписанной в нее сферы, если сторона основания призмы равна 1.

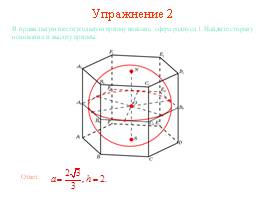
Упражнение 2
В правильную шестиугольную призму вписана сфера радиуса 1. Найдите сторону основания и высоту призмы.

Сфера, вписанная в правильный тетраэдр

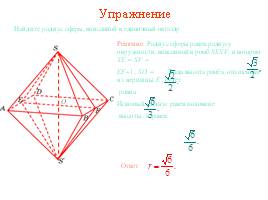
Упражнение 1
Найдите радиус сферы, вписанной в единичный тетраэдр.

Упражнение 2
В правильный тетраэдр вписана единичная сфера. Найдите ребро этого тетраэдра.

Упражнение 3
Найдите радиус сферы, вписанной в правильную треугольную пирамиду, сторона основания которой равна 2, и двугранные углы при основании равны 60о.

Упражнение 4
Найдите радиус сферы, вписанной в правильную треугольную пирамиду, боковые ребра которой равны 1, и плоские углы при вершине равны 90о.

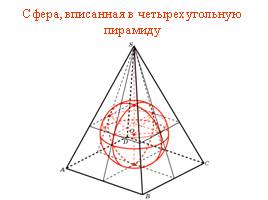
Сфера, вписанная в четырехугольную пирамиду

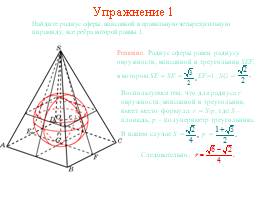
Упражнение 1
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, все ребра которой равны 1.

Упражнение 2
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 1, а боковое ребро - 2.

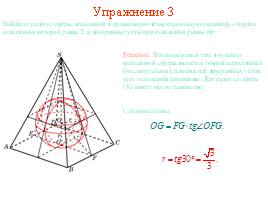
Упражнение 3
Найдите радиус сферы, вписанной в правильную четырехугольную пирамиду, сторона основания которой равна 2, и двугранные углы при основании равны 60о.

Упражнение 4
Единичная сфера вписана в правильную четырехугольную пирамиду, сторона основания которой равна 4. Найдите высоту пирамиды.

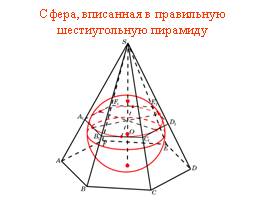
Сфера, вписанная в правильную шестиугольную пирамиду

Упражнение 1
Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду, у которой ребра основания равны 1, а боковые ребра - 2.

Упражнение 2
Найдите радиус сферы, вписанной в правильную шестиугольную пирамиду, у которой ребра основания равны 1, и двугранные углы при основании равны 60о.

Сфера, вписанная в октаэдр

Упражнение
Найдите радиус сферы, вписанной в единичный октаэдр.

Сфера, вписанная в икосаэдр

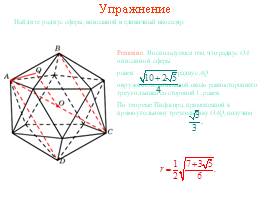
Упражнение
Найдите радиус сферы, вписанной в единичный икосаэдр.

Сфера, вписанная в додекаэдр

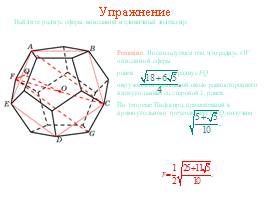
Упражнение
Найдите радиус сферы, вписанной в единичный додекаэдр.

Упражнение 1
Можно вписать сферу в усеченный тетраэдр?

Упражнение 2
Можно вписать сферу в усеченный куб?
Ответ: Нет. Доказательство аналогично предыдущему.

Упражнение 3
Можно вписать сферу в усеченный октаэдр?
Ответ: Нет. Доказательство аналогично предыдущему.

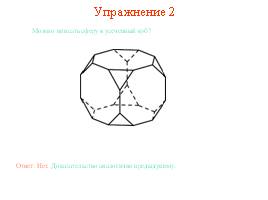
Упражнение 4
Можно вписать сферу в кубооктаэдр?
Ответ: Нет. Доказательство аналогично предыдущему.