Презентация - Задачи «Теория вероятностей»

Теория вероятностей

Презентация предназначена для формирования устойчивых навыков в решении задач по теории вероятностей. Презентация разделена на 3 модуля в соответствии со степенью трудности предлагаемых задач. Каждый модуль содержит теоретический материал и задачи с разобранными решениями.

Случайным называется событие, которое в данный момент может произойти, а может и не произойти. Элементарные события (исходы) – простейшие события, которыми может окончится случайный опыт. Несовместные события – это события, которые не наступают в одном опыте. Классическое определение вероятности. Вероятность события А определяется формулой Р(А)=m/n, где n- количество всех проведенных опытов, m- количество опытов, в которых появилось событие А.
Повторим теорию

В. 3

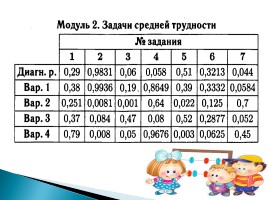
Модуль 2. Задачи средней трудности

Два события А и В называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию А, так и событию В. Пусть событие С означает, что произошло хотя бы одно из событий А и В, тогда С называют объединением событий. Два события А и В называют независимыми, если вероятность каждого из них не зависит от появления или не появления другого события.