Презентация - Сложение целых чисел

Урок 1
Математика 6 класс

Встало солнышко давно, Заглянуло к нам в окно. Нас оно торопит в класс, Математика у нас!

Проверка домашнего задания
№ 540(а), 542(б , г), 543(1-б, 2- а), 545(б), ВИЗ.

09. 10. 16
Классная работа

Хаос не только встречается в жизни, но и среди чисел.
3
-2
-25
-47
-3
6
10
15
-15
63

Разделите числа на две группы по какому-нибудь принципу.
3
-2
-25
-47
-3
6
10
15
-15
63
Положительные числа
Отрицательные числа
Порядок в числах навели

Выполните сложение чисел:
9 + 11 = (- 4) + (- 5) = 5 + (- 3) = (-7) + 4 =

Сложение целых чисел

Знаете ли вы?
Математики древности
Древнегреческий математик Диофант, живший в III .

Знаете ли вы?
Математики древности
Индийский математик Брахмагупта, живший в VII.

Знаете ли вы?
Математики древности
Арабский математик Абу – ль - Вефа, живший в X.

Называли отрицательные числа словами, означавшими «долг», «недостаток», в отличие от «имущества» - положительного числа.

Чтобы понять, по каким правилам складывают целые числа, рассмотрим «денежные» примеры – с доходами и расходами. При этом израсходованные суммы денег будем обозначать отрицательными числами.

(- 4) + (- 5) = ?
Из примера с подсчётом денег легко понять, как складываются отрицательные числа. Если человек израсходовал сначала 4 тыс. р., а затем ещё 5 тыс. р, то общий расход составил 9 тыс. р. Поэтому естественно считать, что (- 4) + (- 5) = - 9 Величину расхода мы определили сложением соответствующих противоположных чисел: 4 + 5 = 9

Правило 1
Сумма двух положительных чисел положительна, а сумма двух отрицательных чисел отрицательна.
стр. 170

А как складывать числа разных знаков?
5 + (- 3) = ? Ясно, что если человек получил денег больше, чем потратил, то его доход окажется положительным. Например, если он получил 5 тыс. р. и потратил 3 тыс. р., то его доход составил 2 тыс. р: 5 + (- 3) = + 2 Величину дохода в этом случае мы нашли вычитанием: 5 – 3 = 2

А как складывать числа разных знаков?
(-7) + 4 = ? Если же человек получил денег меньше, чем ему надо потратить, то его доход выражается отрицательным числом. Например, при доходе 4 тыс. р. и расходе 7 тыс. р., получится убыток, равный 3 тыс. р: (-7) + 4 = - 3 Величину убытка мы также нашли вычитанием: 7 - 4 = 3

Правило 2
Сумма двух чисел разных знаков может быть как положительным числом, так и отрицательным. Знак суммы зависит от того, какое слагаемое «перевесило» - положительное или отрицательное.
стр. 171

Итак, при сложении целых чисел мы работаем в действительности только с соответствующими натуральными числами. Но в одних случаях (когда слагаемые одного знака) мы эти натуральные числа складываем, а в других случаях (когда слагаемые разных знаков) из большего натурального числа вычитаем меньшее.

Представим теперь, что доход и расход были одинаковы, например по 10 тыс. р. Очевидно, что в этом случае прибыль равна нулю. Поэтому (+ 10) + (- 10) = 0

Правило 3
Сумма противоположных чисел равна 0: а + ( - а) = 0.
стр. 171

Наконец, правило сложения целого числа с нулём такое же, как и для натуральных чисел. а + 0 = 0 + а = а. Например, (- 43) + 0 = - 43, 0 + (- 18) = - 18. Заметим, что действие сложения целых чисел, как и действие сложения натуральных чисел, обладает переместительным и сочетательным свойствами. Эти свойства позволяют переставлять слагаемые и объединять их в группы.

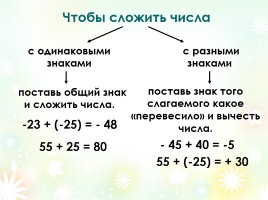
Чтобы сложить числа
с одинаковыми знаками
с разными знаками
поставь общий знак и сложить числа.
поставь знак того слагаемого какое «перевесило» и вычесть числа.
-23 + (-25) = - 48
55 + 25 = 80
- 45 + 40 = -5
55 + (-25) = + 30

-5 + (-32) =
-37
-27
47
Чтобы сложить числа
с одинаковыми знаками
с разными знаками
поставь общий знак и сложить числа.
поставь знак того слагаемого какое «перевесило» и вычесть числа.

Подумай ещё раз

Молодец

85 + (-25) =
60
110
-60
Чтобы сложить числа
с одинаковыми знаками
с разными знаками
поставь общий знак и сложить числа.
поставь знак того слагаемого какое «перевесило» и вычесть числа.

Подумай ещё раз

Молодец

- 48 + 15 =
-33
33
-62
Чтобы сложить числа
с одинаковыми знаками
с разными знаками
поставь общий знак и сложить числа.
поставь знак того слагаемого какое «перевесило» и вычесть числа.

Подумай ещё раз

Молодец

- 26 + (- 6) =
- 70 + 50 =
17 + (-30) =
80 + 120 =
- 63 + (-73) =
-32
-20
-13
200
-136
12
15
120
136
Сложение отрицательных чисел
Сложение положительных чисел
Сложение чисел с разными знаками

Работа с учебником
№ 546, 547 (первые два столбика), 548 (1-а, 2 –г, д , е), 550 – 551 (а , в) .

Самостоятельная работа
1 вариант 2 вариант
-7 + (-9) = 37 + (-56) = -43 + 75 = 17 + 18 = -35 + (-24) = 40 + (-67) = -69 + 84 = 83 + 29 =
-59 112 -16 35 35 -27 -19 -25 112 32 -45 15
З Щ Х В С Н А Ф К О Ц А

Домашнее задание
Прочитать, разобрать и выучить правила из n 36, фрагмент 1. Решить задания: № 546 - 547 (последний столбик), 548 (1 – б, 2 а - в), 550 – 551(б , г).

1. С чего начался наш урок?
2. Где возникла трудность?
3. Как нашли решение?
4. Какую цель ставили перед собой?
5. Цель достигнута?
Рефлексия