Слайды и текст этой онлайн презентации
Слайд 1
Тема урока:
Соотношения между сторонами и углами в прямоугольном треугольнике
2013 год
8 класс
ГБООУ «Медновская санаторная школа-интернат»
Моляков Александр Вячеславович
Слайд 2
Цели урока:
Научиться применять знания синуса, косинуса, тангенса
и котангенса при решении задач различной сложности.
Уметь устанавливать связь изучаемого материала с ранее
пройденным.
Научиться применять знания в практической деятельности
человека.
Учиться: - проявлять настойчивость в достижении
цели;
- работать в коллективе;
- контролировать и оценивать свою
работу на уроке.
5. Учиться грамотно формулировать свои мысли.
Слайд 3
«Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет»
Лейбниц
Слайд 4
Чтобы не ошибиться при строительстве пирамиды, древние
египтяне прежде всего размечали на земле ее основание в виде квадрата. Прямые углы такого квадрата они «чертили» с помощью веревки. Но веревка была не простая. На ней завязывали узлы, делившие ее на 12 равных частей. Веревку натягивали в виде треугольника со сторонами, отношение между которыми равнялось 3 : 4 : 5. Угол, противоположный самой длинной стороне, всегда оказывался прямым. Почему? Это объясняет теорема Пифагора, самая популярная, быть может, из всех теорем.
Слайд 5
Прямоугольный треугольник имеет широкое применение в повседневной жизни, многие геометрические и практические задачи сводятся к вычислению элементов прямоугольного треугольника, другими словами, к решению прямоугольного треугольника.
Решение прямоугольных треугольников с помощью
синуса, косинуса, тангенса и котангенса острого угла.
Слайд 6
А
В
С
с
в
а
Какой треугольник называется прямоугольным?
Как называются стороны прямоугольного треугольника?
Назовите катет, противолежащий углу А.
Какой катет является прилежащим к углу В?
Какое отношение называется синусом острого угла
прямоугольного треугольника?
Дайте определение косинуса острого угла прямоугольного треугольника.
Что называется тангенсом острого угла прямоугольного треугольника?
Установи соответствие:
sin 45° 2. cos 30° 3. tg 60° 4. ctg45°
1. 2. 3. 4. 1 5.
Слайд 7
Установите, истины или ложны следующие высказывания:
1.
М
К
N
MN – катет, прилежащий к углу К.
2.
АС – катет, противолежащий углу В.
В
С
А
3. Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
Котангенсом острого угла прямоугольного треугольника
называется отношение противолежащего катета к гипотенузе.
Синусом острого угла прямоугольного треугольника
называется отношение противолежащего катета к
прилежащему.
6.
А
В
С
5
12
13
Sin A = .
5
13
7.
К
S
D
Ctg К = .
SK
SD
Л
И
И
Л
Л
И
И
Слайд 8
№1.
Дано: ∆ АВС, угол С =90°, угол А = 41°, ВС = 5.
Найти: АС.
А. 5· cos 41° Б. В. 5 · tg 41° Г.
5
tg 41°
5
sin 41°
№2.
Дано: sin α = . Найти tg α.
А. Б. В. Г.
12
13
12
5
13
12
12
5
12
13
№3.
В ∆ АВС угол С = 90°, CD – высота, угол А = α, АВ = k.
Найти АС, ВС, AD.
№4.
В прямоугольной трапеции меньшее основание равно 6,
А меньшая боковая сторона 2√3.
Найти площадь трапеции, если один из ее углов
Равен 120°.
АС = k · cos α
BC = k · sin α
AD = k · cos ² α
S = 14 √3.
Слайд 9
Решение задачи №4:
120°
А
В
С
D
2√3
6
H
Дано: АВСD – прямоугольная трапеция,
ВС = 6 см, АВ = 2√3, угол ВСD = 120°.
Найти: S трапеции.
Решение: S = · CH.
Проведем высоту СН, СН = АВ = 2√3.
Угол HCD = 30°.
В ∆ CDH HD = CH · tg 30° = 2√3 · 1/ √3 = 2,
АН = 6, сл – но AD = 2 + 6 = 8.
S = · 2√3 = 14√3.
Ответ : 14√3 см².
BC + AD
2
6 + 8
2
Слайд 10
Для постройки лестницы на второй этаж требуется купить доски
в количестве, равном количеству ступенек. Подсчитайте , какое
количество досок необходимо купить, если известно, что высота
между этажами равна 3 метра, угол наклона лестницы равен 37°,
а ширина доски – 0,25 м.
Применение знаний в практической жизни.
Слайд 11
Вариант расположения
ступенек:
Слайд 12
Один из способов решения:
3 метра = 300 сантиметров.
0,25 метра = 25 сантиметров.
300 : sin 37° = 500 (см)
500² - 300² = 160000
= 400 (см)
400 : 25 = 16 ( ступенек)
Ответ: потребуется купить
16 досок.
Слайд 13
Подсчитай набранные баллы
и оцени свою работу на уроке:
16 – 19 баллов……………… «5»
12 – 15 баллов……………… «4»
7 – 11 баллов……………… «3»
Слайд 14
Домашнее задание:
Стандарт № 9, 10, 11.
Хорошо № 20, 22.
Отлично № 29, 30.
Слайд 15
Закончи предложение:
Сегодня на уроке я запомнил……………..
Я научился……………………………………
Я понял……………………………………......
У меня не получилось………………………
Мне бы хотелось…………………………….
Я справлюсь с домашней работой………...
 Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника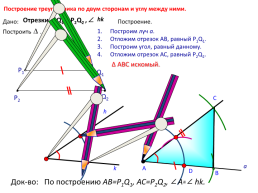 Построение треугольника по двум сторонам и углу между ними
Построение треугольника по двум сторонам и углу между ними Решение задач по теме «Прямоугольный треугольник»
Решение задач по теме «Прямоугольный треугольник» Прямоугольный треугольник
Прямоугольный треугольник Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства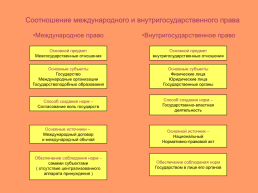 Соотношение международного и внутригосударственного права. Международное право
Соотношение международного и внутригосударственного права. Международное право Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
















