Презентация - Золотое сечение вокруг нас

МАЛАЯ АКАДЕМИЯ НАУК МБОУ «ЮЖНО-РОССИЙСКИЙ ЛИЦЕЙ КАЗАЧЕСТВА И НАРОДОВ КАВКАЗА» ГОРОДА-КУРОРТА ЖЕЛЕЗНОВОДСКА СТАВРОПОЛЬСКОГО КРАЯ   IX ОТКРЫТАЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ КОНФЕРЕНЦИЯ ШКОЛЬНИКОВ Секция: Математика
«Золотое сечение вокруг нас» Выполнил: Черников Евгений, ученик 7 “б” класса Научный руководитель: Ермуратина Татьяна Викторовна учитель математики высшей категории п.Иноземцево 2013

Великие учёные

Золотое сечение в природе

Золотое сечение в природе

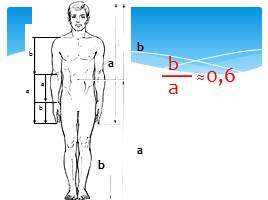
В телосложении человека

Понятие «Золотое сечение»
a : b = b : c или с : b = b : а
Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

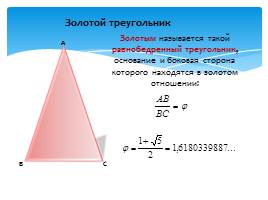
Эта пропорция равна:
Золотое сечение в процентах

А
В
С
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении:
Золотой треугольник

Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ, называется золотым прямоугольником.
Золотой прямоугольник

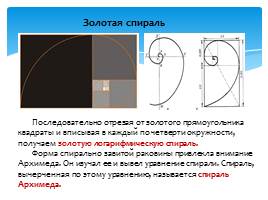
Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, получаем золотую логарифмическую спираль. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.
Золотая спираль

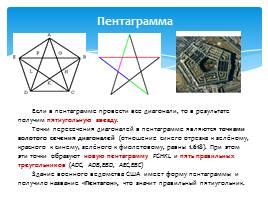
Пентаграмма
Если в пентаграмме провести все диагонали, то в результате получим пятиугольную звезду. Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC) Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.

Феномен роста и развития

Пропорции золотого сечения в строении стрекозы
а
b
b: a= 0,618

Золотое сечение в архитектуре

ПАРФЕНОН
0,618

Леонардо да Винчи

b
a
a
b

b
a
≈
0,6

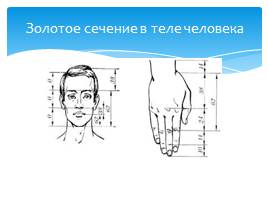
Золотое сечение в теле человека

Эксперимент №1

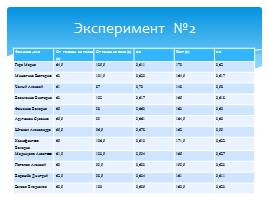
Эксперимент №2
Фамилия ,имя От головы до талии (в) От талии до пола (а) в/а Рост (с) с/в
Гиря Мария 64,5 105,5 0,611 170 0,62
Мишагина Екатерина 63 101,5 0,620 164,5 0,617
Чалый Алексей 61 87 0,70 148 0,58
Василенко Виктория 63 102 0,617 165 0,618
Фоменко Валерия 65 98 0,663 163 0,60
Арутюнян Сусанна 65,5 99 0,661 164,5 0,60
Штокол Александра 65,5 96,5 0,678 162 0,59
Ксенофонтова Валерия 65 106,5 0,610 171,5 0,622
Мединцева Анастасия 61,5 103,5 0,594 165 0,627
Потапов Алексей 60 99,5 0,603 159,5 0,623
Ворожба Дмитрий 62,5 98,5 0,634 161 0,611
Беляев Владислав 60,5 100 0,605 160,5 0,623

Эксперимент №2

Спасибо за внимание!