Презентация - Задачи на производную

Задачи на производную
Автор: Цыбикова Сэндэма Дугаровна учитель СОСОШ№2 с.Сосново-Озёрское

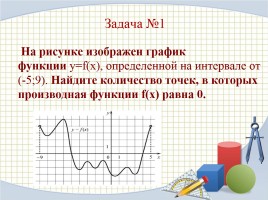
Задача №1
 На рисунке изображен график функции y=f(x), определенной на интервале от (-5;9). Найдите количество точек, в которых производная функции f(x) равна 0.

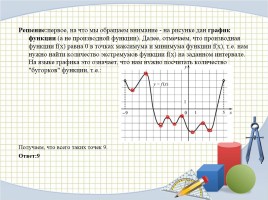
Решение:первое, на что мы обращаем внимание - на рисунке дан график функции (а не производной функции). Далее, отмечаем, что производная функции f(x) равна 0 в точках максимума и минимума функции f(x), т.е. нам нужно найти количество экстремумов функции f(x) на заданном интервале. На языке графика это означает, что нам нужно посчитать количество "бугорков" функции, т.е.: Получаем, что всего таких точек 9. Ответ:9

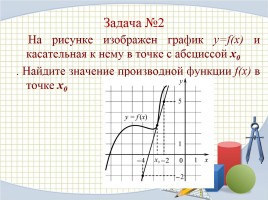
На рисунке изображен график y=f(x) и касательная к нему в точке с абсциссой х0 . Найдите значение производной функции f(x) в точке х0
Задача №2

Решение:Значение производной функции f(x) в точке касания равно угловому коэффициенту касательной. Поэтому нам надо составить уравнение данной касательной и графику и найти угловой коэффициент. В общем случае, уравнение касательной имеет вид: y = kx+b. В этом уравнении k и есть тот самый угловой коэффициент, который мы будет искать. На рисунке жирными точками отмечены точки, через которые проходит наша касательная. Координаты этих точек: (-4; -2) и (-2; 5). Так как данная прямая проходит через эти точки, то подставим их координаты в уравнение касательной и найдем значение коэффициента k. y = kx+b -2 = -4k+b (подставили точку с координатами (-4;-2)); 5 = -2k+b (подставили точку с координатами (-2;5)). Теперь вычитаем из первого уравнения второе: -2 - 5 = -4k-(-2k); -7 = -2k; k = 7/2 = 3,5. Получаем искомое значение k=3,5, что то же самое, что значение производной функции f(x) в точке x_0. Ответ: 3,5. .
y = kx+b -2 = -4k+b (подставили точку с координатами (-4;-2)); 5 = -2k+b (подставили точку с координатами (-2;5)). Теперь вычитаем из первого уравнения второе: -2 - 5 = -4k-(-2k); -7 = -2k; k = 7/2 = 3,5. Получаем искомое значение k=3,5, что то же самое, что значение производной функции f(x) в точке      .   Ответ: 3,5.  

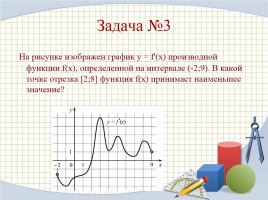
Задача №3
На рисунке изображен график y = f'(x) производной функции f(x), определенной на интервале (-2;9). В какой точке отрезка [2;8] функция f(x) принимает наименьшее значение?

Решение:Если график y = f'(x) производной функции f(x) пересекает ось Ox в некоторой точке, то функция f(x) в этой точке имеет максимум или минимум. В данном случае график y = f'(x) перескает ось Ox в точке x=2. Так как при x<2 функция y = f'(x) <0 (это видно из графика), а при x>2 y = f'(x)>0 на рассматриваемом графике, то знак производной переходит с "-" на "+". А это означает, что x=2 - точка минимума. И т.к. x=2 принадлежит отрезку [2;8], то x=2 - искомая точка, в которой функция принимает наименьшее значение. Ответ: 2. Ответ

Задача №4
На рисунке изображен график функции y=f'(x) - производной функции f(x), определенной на интервале от (-6;5). В какой точке отрезка [-5;-1] функция f(x) принимает наибольшее значение?

На отрезке [-5;-1] производная f'(x) принимает отрицательные значения, а значит на этом отрезке функция f(x) убывает. Если функция убывает на заданном отрезке, то наибольшее значение она принимает в наименьшей точке отрезка, т.е. в точке -5. Ответ: -5.

Задача №5
На рисунке изображен график функции y=f'(x) - производной функции f(x), определенной на интервале от (-6;5). В какой точке отрезка [-3;4] функция f(x) принимает наибольшее значение?.

График производной пересекает ось Ox в точке -1. Эта точка принадлежит отрезку [-3;4] и является точкой экстремума функции f(x). Ответ: -1. Так как график производной переходит в этой точке с "+" на "-", то это точка максимума, а значит наибольшее значение на отрезке [-3;4] функция f(x) принимает именно в этой точке.

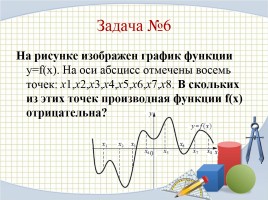
Задача №6
На рисунке изображен график функции y=f(x). На оси абсцисс отмечены восемь точек: x1,x2,x3,x4,x5,x6,x7,x8. В скольких из этих точек производная функции f(x) отрицательна?  

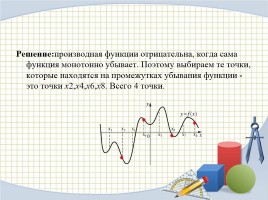
Решение:производная функции отрицательна, когда сама функция монотонно убывает. Поэтому выбираем те точки, которые находятся на промежутках убывания функции - это точки x2,x4,x6,x8. Всего 4 точки.

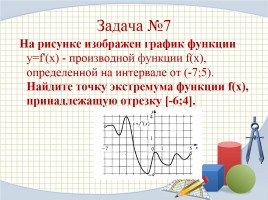
Задача №7
На рисунке изображен график функции y=f'(x) - производной функции f(x), определенной на интервале от (-7;5). Найдите точку экстремума функции f(x), принадлежащую отрезку [-6;4].

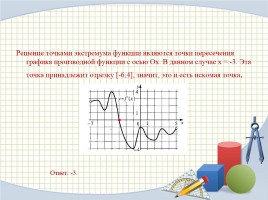
Решение:точками экстремума функции являются точки пересечения графика производной функции с осью Ox. В данном случае x = -3. Эта точка принадлежит отрезку [-6;4], значит, это и есть искомая точка.
Ответ: -3.

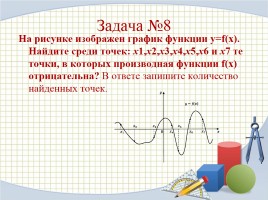
Задача №8
На рисунке изображен график функции y=f(x). Найдите среди точек: x1,x2,x3,x4,x5,x6 и x7 те точки, в которых производная функции f(x) отрицательна? В ответе запишите количество найденных точек.

Решение: производная функции отрицательна, когда сама функция монотонно убывает. Поэтому выбираем те точки, которые находятся на промежутках убывания функции - это точки x1,x2,x4,x6,x7. Всего 5 точек. Ответ  

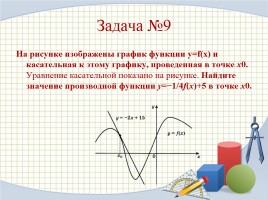
Задача №9
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведенная в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции y=−1/4f(x)+5 в точке x0.  

Найдем производную функции y=−1/4f(x)+5в точке x0: y′=−1/4f′(x0) Так как уравнение касательной к функции f(x) в точке x0 имеет вид: y = -2x+5, то f′(x0)=−2. Тогда искомая производная равна: y' = −1/4⋅(−2)=0,5.   Ответ: 0,5.  

Задача №10
На рисунке изображен график функции y=f'(x) - производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) перпендикулярна прямой y = -2x-11.

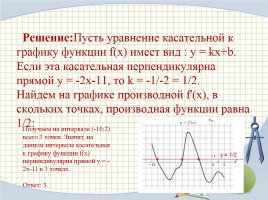
Решение:Пусть уравнение касательной к графику функции f(x) имеет вид : y = kx+b. Если эта касательная перпендикулярна прямой y = -2x-11, то k = -1/-2 = 1/2. Найдем на графике производной f'(x), в скольких точках, производная функции равна 1/2:
Получаем на интервале (-10;2) всего 3 точки. Значит, на данном интервале касательная к графику функции f(x) перпендикулярна прямой y = -2x-11 в 3 точках.   Ответ: 3.

Сайт: http://pedsovet.su/ http://mathexam.ru/b8/b8_5.html