Презентация - Решение задач ОГЭ «Модуль геометрия» Часть 2

Выступление на РМО учителей математики по теме: 
Решение задач ОГЭ «Модуль геометрия» часть 2
Копанева Нэля Николаевна - учитель математики 1 квалификационной категории МОБУ «Кузнецовская средняя общеобразовательная школа»
с.Кузнецово, 2016 г.

Вступление
Проблема – как подготовить выпускников к успешной сдаче экзамена встаёт перед каждым учителем. Основная подготовка выпускников к ОГЭ по математике осуществляется не только в течение всего учебного года в старшей школе, но и раньше, начиная с 7 класса. Исключительно важным становится целенаправленная и специально планируемая подготовка школьников к ОГЭ. Безусловно, на последние годы обучения в школе приходится максимальная нагрузка на учащихся. При этом возрастает роль и ответственность в подготовительной работе и учителя, и самого ученика. Моя цель, как учителя, помочь ребёнку в подготовке к ГИА, разобраться в самых значимых моментах в подготовительной работе, знать существующую документацию по проведению экзамена.

Задачи по подготовке учащихся к ОГЭ:
1. Начинать подготовку к итоговой аттестации с 5 класса; 2. Создавать учебный материал (по типу ГИА) и использовать готовые печатные и электронные пособия; 3. Учить школьников ≪технике сдачи теста≫; 4. Психологический настрой к ГИА; 5. Через систему дополнительных занятий ( факультативов, курсов, индивидуальных консультаций) повышать интерес к предмету и личную ответственность школьника за результаты обучения.

Как я строю свою работу по подготовке учащихся к сдаче экзамена по математике в форме ГИА?
1) провожу исследование демо-версий ГИА по математике последних лет, взятые на сайте www. fipi. ru, http://rcoi12.ru/gia9/ - организация ГБУ Республики Марий Эл "ЦИТОКО" . Анализирую результаты прошлых лет, делаю выводы. 2) соотношу своё календарно-тематическое планирование в данных классах с темами, используемыми в КИМах. Затем произвожу отбор тех заданий, работу над которыми уже можно начинать в 7-8 классах. 3) осуществляю подбор необходимой литературы: дидактические материалы, тесты и др. 4) В зависимости от класса, учащихся можно разбить на группы. Чтобы строить работу дифференцированно, не забывая об учащихся с повышенной мотивацией и слабоуспевающих, проводя индивидуальные консультации. Рекомендую использование Интернет-ресурсов для самостоятельной домашней подготовки к экзамену. Слабоуспевающим ученикам не всегда удаётся справиться с предлагаемыми заданиями в классной и домашней работе. С ними отрабатываем те задания, которые вызывают затруднения. Решаю с ними примеры и задачи подобного характера. Эти меры необходимы, для преодоления ими «нижнего порога» на ГИА.

Предлагаю решение задач ОГЭ «Модуль геометрия» часть 2 вариант 261 диагностического тестирования.

Вариант 261 № 24
Катет и гипотенуза прямоугольного треугольника равны 35 и 125. Найдите высоту, проведенную к гипотенузе.

№ 24
1 сп. 1) AB - гипотенуза, BC - катет. Найдем AC по теореме Пифагора: AB2=BC2+CA2 1252=352+CA2 15625=1225+CA2 14400=CA2 CA=120 2) Вычислим площадь треугольника АВС S = ½ * СВ* АС S = ½ * 35 * 120 = 2100 3) Воспользуемся формулой площади треугольника S = ½ * АВ *СД 2100 = ½ * 125 * СД СД = 4200 : 125 = 33,6 Ответ: СД= 33,6
2 сп. 1) AB - гипотенуза, BC - катет. Найдем AC по теореме Пифагора: AB2=BC2+CA2 1252=352+CA2 15625=1225+CA2 14400=CA2 CA=120 2) Для Δ ABC sin A= СВ/АВ = 35/125 = 7/25 3) Для Δ ACD sin A= СД/СА CД=AC*sin A=120* 7/25 = 33,6 Ответ: СД= 33,6

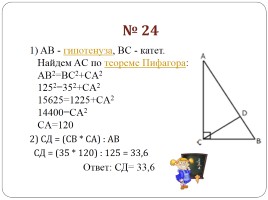
№ 24
1) AB - гипотенуза, BC - катет. Найдем AC по теореме Пифагора: AB2=BC2+CA2 1252=352+CA2 15625=1225+CA2 14400=CA2 CA=120 2) СД = (СВ * СА) : АВ СД = (35 * 120) : 125 = 33,6 Ответ: СД= 33,6

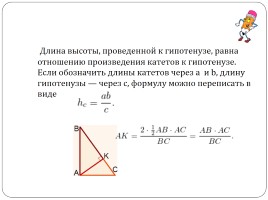
Длина высоты, проведенной к гипотенузе, равна отношению произведения катетов к гипотенузе. Если обозначить длины катетов через a  и b, длину гипотенузы — через с, формулу можно переписать в виде   

№ 25
Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и ADB подобны. ABCD - трапеция, следовательно, AD||BC. ∠CBD=∠ADB (т.к. это накрест-лежащие углы  для параллельных прямых AD и BC и секущей ВД). Рассмотрим отношения сторон: BC/BD= 5/45=1/3 BD/AD=15/45=1/3 Тогда по второму признаку подобия треугольников, треугольники CBD и ADB подобны.

№ 26
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=8, BC=7.

№ 26
1 сп. По условию задачи AB перпендикулярна BC, следовательно перпендикулярна и AD (т.к. в трапеции основания параллельны). Расстояние от точки Е до прямой CD - отрезок, перпендикулярный CD и проходящий через точку Е. 1) Рассмотрим треугольники TCB и CKD. ∠CTB=∠DCK (т.к. это соответственные углы при параллельных прямых TA и CK) ∠TBC=∠CKD=90° Следовательно, эти треугольники подобны (по первому признаку подобия). Тогда, BC/KD=TC/CD 7/1=TC/CD TC=7 *CD По теореме о касательно и секущей: TE2=TD*TC=(TC+CD)*TC=(7*CD+CD)*7*CD=8*CD*7*CD= = 56*CD2 TE=CD*√56=2*CD*√14 Рассмотрим треугольники TEF и TAD. ∠CTB - общий ∠EFT=∠TAD=90° Следовательно, применив теорему о сумме углов треугольника, получаем, что ∠TEF=∠ADT. Следовательно, cos∠TEF=cos∠ADT. EF=TE*cos∠TEF=TE*cos∠ADT=TE/CD=2*CD*√14/CD=2√14 Ответ: EF=2√14

№ 26
2 сп. Рассмотрим многоугольник ЕВСК и DАЕК, они подобны, т.к. <ЕВС =

Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA*MB.

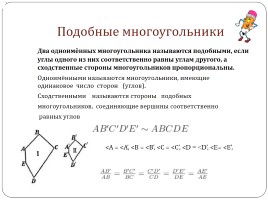
Подобные многоугольники
Два одноимённых многоугольника называются подобными, если углы одного из них соответственно равны углам другого, а сходственные стороны многоугольников пропорциональны. Одноимёнными называются многоугольники, имеющие одинаковое  число  сторон   (углов). Сходственными    называются стороны   подобных    многоугольников,  соединяющие вершины соответственно равных углов
.
<А = <А’, <В = <В’, <С = <С’,

В этом году готовлю учащихся 9 класса к сдаче ОГЭ. В течение учебного года провожу инструктажи по заполнению бланков, ознакомлению учащихся с демовариантом ОГЭ, правилами поведения на экзамене.

Для того чтобы наглядно видеть уровень подготовленности выпускников к сдаче ГИА результаты выполнения диагностических и тренировочных работ отражаются в таблице.

Мониторинг результатов

Полезные ссылки для подготовки к ОГЭ-2016
http://www.fipi.ru/ -«Федеральный институт педагогических измерений»  http://rcoi12.ru/gia9/ - Организация ГБУ Республики Марий Эл "ЦИТОКО" http://infourok.ru/- инфоурок http://www.metod-kopilka.ru/- метод-копилка mathgia.ru – открытый банк заданий ГИА по математике   sdamgia.ru –образовательный портал для подготовки к ГИА  по многим предметам   http://alleng.ru/ Всем, кто учится. Очень много образовательной литературы      http://aksioma72.blogspot.ru/ -блог учителя математики Продан С.В.

http://www.fipi.ru/ - ФИПИ

http://rcoi12.ru/gia9/ - Организация ГБУ Республики Марий Эл "ЦИТОКО"

http://mathgia.ru/or/gia12/ - открытый банк заданий по математике

http://www.uchportal.ru/video/vic/ogeh_gia_po_matematike/zadacha_24- учительский портал

http://reshuoge.ru/- решу ОГЭ

http://egeigia.ru/all-gia/materialy-gia/matematika- ЕГЭ /ОГЭ от урока до экзамена

http://otvet-gotov.ru/- ответ готов

Интернет ресурсы
http://nsportal.ru/ - социальная сеть работников образования http://otvet-gotov.ru/- - ответ готов (картинки) http://go.mail.ru/- картинки дети

Спасибо за внимание!

Данная работа предназначена для учителей и учащихся при подготовке к ОГЭ. Рассматриваются три задачи части 2 диагностического ОГЭ с различными способами решения, с целью выбора более подходящего вам решения.