Презентация - Экономические задачи на ЕГЭ по математике

Экономические задачи на ЕГЭ по математике
Автор работы: Зубарева Н.С.-учитель математики МОУ СОШ №2

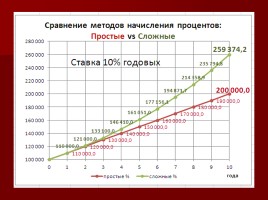
Банковская система России
20150913213012_2.jpg

Схемы выплаты пользовательских кредитов
Аннуитетная Дифференцированная Буллитная

В чем различие?

Способы решения задач с «экономическим содержанием»
Решение задач по формулам Решение задач в общем виде Применение свойства степеней Решение задач с помощью математического анализа Задачи на сравнение

Задача №1
31 декабря 2013 года Андрей взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), а затем Андрей переводит в банк 3 460 600 рублей. Какую сумму взял Андрей в банке, если он выплатил долг тремя равными платежами (то есть за 3 года)?

Задача №2
1 января 2015 года пенсионерка взяла в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 3 процента на оставшуюся сумму долга (то есть увеличивает долг на 3%), а затем пенсионерка переводит в банк платеж. На какое минимальное количество месяцев пенсионерка может взять кредит, чтобы ежемесячные платежи составили не более 220 тыс. рублей?

Задача №3
Бриллиант массой 20 карат был разбит на две части, после чего его стоимость уменьшилась на 25,5 %. а) Найдите массы частей, на которые был разбит бриллиант, если известно, что цена бриллианта пропорциональна квадрату его массы. б) На какое максимальное число процентов может уменьшиться цена бриллианта, разбитого на две части?

Задача №4
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2часов в неделю, то за эту неделю они производят 3tединиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2часов в неделю, то за эту неделю они производят 4tединиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделить 5000000 рублей в неделю на оплату труда рабочих.Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Советы и рекомендации
Необходимо знать: 1.Все о процентах. 2.Формулы прогрессии. 3.Признаки делимости. 4.Метод прикидки. 5.Метод оценки. 6.Экономические термины. 7.Таблица умножения.

С Наступающим новым годом!
Спасибо за внимание!