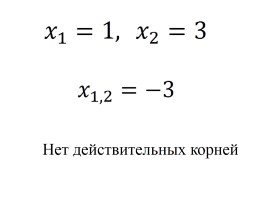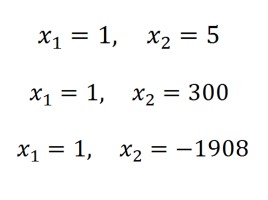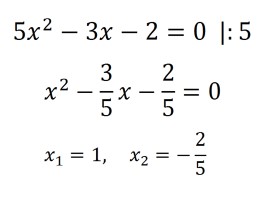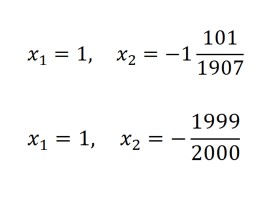Презентация - Квадратные уравнения (вопросы, задачи, конкурсы)

Уравнения второй степени умели решать в Древнем Вавилоне во втором тысячелетии до нашей эры. Но знания вавилонян в этом вопросе не повлияли на развитие европейской науки. Достижения восточных народов долго оставались в Европе неизвестными.

Кто из европейских ученых одним из первых начал решать квадратные уравнения? Выполнив задание, вы узнаете ответ на этот вопрос.

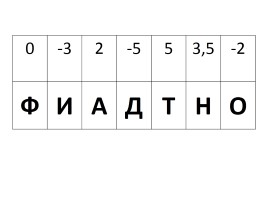
Задание 1. Решите неполные квадратные уравнения

Расположите полученные корни по возрастанию и замените каждое число соответствующей буквой. Прочитайте слово.

0 -3 2 -5 5 3,5 -2
Ф И А Д Т Н О

Диофант - древнегреческий математик из Александрии

Герон Александрийский

Диофант и Герон указали приемы, совпадающими с нашими способами решения квадратных уравнений. В работах индийских и китайских математиков, написанных первых веках нашей эры, встречаются отрицательные корни квадратных уравнений.

Бхаскара-индийский математик (XIIв.) «Люди отрицательных корней не одобряют»

Большие заслуги в развитии учения о квадратных уравнениях имеет среднеазиатский математик Аль-Хорезми

Он показал вывод правила решения квадратного уравнения, который излагается доныне в учебниках.

Формулами для решения квадратных уравнений владел Леонардо Пизанский в начале XIIIв.

Изучал квадратные уравнения и Ф. Виет, но он признавал только положительные корни

В XVI в. итальянские математики Д. Кардано, Л. Феррари, Н. Тарталья присоединили к положительным корням уравнения отрицательные.

Задание 2 Сколько корней имеет квадратное уравнение? Решите его

Нет действительных корней

Специальные способы решения квадратных уравнений

Задание 3 Решите уравнения новым способом

Задание 4. Попробуйте решить:

Благодарю за внимание, за участие в нашей конференции.