Презентация - Система линейных уравнений с двумя переменными

Система линейных уравнений с 2 переменными

«Математику нельзя изучать, наблюдая как это делает сосед»

2x-y=1
Что записано на экране?

2x-y=1
Что записано на экране? Ответ: Линейное уравнение с двумя переменными.

2x-y=1
Что называется решением уравнения с двумя переменными?

2x-y=1
Что называется решением уравнения с двумя переменными? Ответ. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

Что называется графиком уравнения двумя переменными?

Что называется графиком уравнения с двумя переменными? Ответ: Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения.

Что является графиком линейного уравнения с двумя переменными?

Что является графиком линейного уравнения с двумя переменными? Ответ: Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

2x-y=1
Как узнать будет ли пара (1;1), (1;5) решением уравнения?

2x-y=1
Как узнать будет ли пара (1;1), (1;5) решением уравнения? Ответ: 2·1-1=1 верно Пара (1;1) является решением уравнения

2x-y=1
Как узнать будет ли пара (1;1), (1;5) решением уравнения? Ответ: 2·1-1=1 верно Пара (1;1) является решением уравнения 2·1-5=1 неверно Пара (1;5) не является решением уравнения

2x-y=1
Найти три решения данного уравнения.

Выразить переменную y через переменную x.
а) x + y = 4; б) 2x – y = 2; в) x + 2y = 4; г) x – y = 0.

Выразить переменную y через переменную x.
а) x + y = 4; y = 4 - x б) 2x – y = 2; y = 2x - 2 в) x + 2y = 4; y = 2 – 0,5x г) x – y = 0. y = x

При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8

При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8 Ответ: при k= -6 и b ≠8

При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8 Ответ: при k= -6 и b ≠8 б) пересекает график функции y= -6x+8

При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8 Ответ: при k= -6 и b ≠8 б) пересекает график функции y= -6x+8 Ответ: при к ≠ -6

При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8 Ответ: при k= -6 и b ≠8 б) пересекает график функции y= -6x+8 Ответ: при к ≠ -6 в) совпадает с графиком функции y=-6x+8

При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8 Ответ: при k= -6 и b ≠8 б) пересекает график функции y= -6x+8 Ответ: при к ≠ -6 в) совпадает с графиком функции y=-6x+8 Ответ: при k= -6 и b=8

Задача. Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.

Задача. Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.
Обозначим первое число буквой x, а второе буквой y. По условию задачи сумма чисел равна 12, т.е. x+y=12. Так как разность чисел равна 2, то x – y =2.

Система уравнений - это
несколько уравнений, в которых одни и те же буквы обозначают одни и те же числа. Или – несколько уравнений, для которых надо найти общие решения.

Решение системы уравнений с двумя переменными - это
пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Что называют системой уравнений?
Рассмотрим два линейных уравнения: Y=-x+3 и Y=2x-3 Найдём такую пару значений (x;y), которая одновременно является решением и первого и второго уравнения При x=2 и y=1 и первое и второе уравнения превращаются в верные равенства. 1 = -2+3 и 1 = 2∙2 -3 То, есть пара (2; 1) является общим решением этих уравнений.

Решить систему уравнений - это найти их общие решения
Поиск общего решения нескольких уравнений называют решением системы уравнений. Уравнения записывают друг под другом и обозначают фигурной скобкой y=-x+3 y=2x-3 А ответ записывают в виде пары (x;y) Ответ: (2;1)

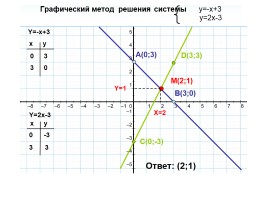
Графический метод решения системы y=-x+3 y=2x-3
Y=-x+3
Y=2x-3
x
y
0
3
x
y
0
3
3
0
-3
3
A(0;3)
B(3;0)
C(0;-3)
D(3;3)
M(2;1)
X=2
Y=1
Ответ: (2;1)

Правило решения системы графическим способом:
Построить график каждого из уравнений системы; 2) Найти координаты точки пересечения построенных прямых (если они пересекаются)

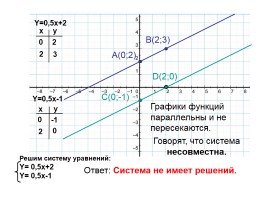
Y=0,5x-1
Y=0,5x+2
x
x
y
y
0
2
2
3
0
-1
2
0
A(0;2)
B(2;3)
C(0;-1)
D(2;0)
Решим систему уравнений: Y= 0,5x+2 Y= 0,5x-1
Графики функций параллельны и не пересекаются.
Говорят, что система несовместна.
Ответ: Система не имеет решений.

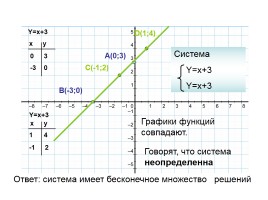
Y=x+3
Y=x+3
x
y
0
-3
x
y
1
-1
3
0
4
2
A(0;3)
B(-3;0)
C(-1;2)
D(1;4)
Система Y=x+3 Y=x+3
Графики функций совпадают.
Говорят, что система неопределенна
Ответ: система имеет бесконечное множество решений

Алгоритм нахождения количества системы уравнений с 2 переменными
1) Из каждого уравнения выразить y через х. 2)
Если к1 к2 Графики пересекаются Система имеет единственное решение
Если к1=к2, b1 b2 Графики параллельны Система не имеет решений
Если к1=к2, b1=b2 Графики совпадают Система имеет бесконечно много решений

Является ли пара чисел решением системы
(3;1)
(2;2)
верно
неверно
верно
верно
(3;1) не является решением
(2;2) является решением

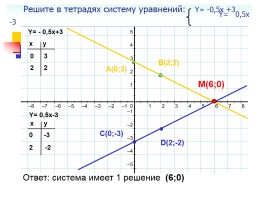
Решите в тетрадях систему уравнений: Y= -0,5x +3 Y= 0,5x -3
Y= - 0,5x+3
Y= 0,5x-3
x
y
0
2
x
y
0
2
3
2
-3
-2
A(0;3)
B(2;2)
C(0;-3)
D(2;-2)
M(6;0)
Ответ: система имеет 1 решение (6;0)

Алгоритм нахождения количества системы уравнений с 2 переменными
1) Из каждого уравнения выразить y через х. 2)
Если к1 к2 Графики пересекаются Система имеет единственное решение
Если к1=к2, b1 b2 Графики параллельны Система не имеет решений
Если к1=к2, b1=b2 Графики совпадают Система имеет бесконечно много решений

Выяснить, сколько решений имеет система.
1 вариант 2 вариант

Проверка 1 варианта
к1 = к2= - 0,5 b1 b2
Система не имеет решений
к1 к2
Система имеет единственное решение

Проверка 2 варианта
к1 к2
Система имеет единственное решение
к1=к2, b1=b2
Система имеет бесконечно много решений

Домашнее задание: п.42 (определение, примеры) № 1058, № 1061 № 1063, №1067(а)

Система линейных уравнений с 2 переменными
k1 = -1 k2 = 1