Презентация - Подготовка к ОГЭ - Задание №16

ПОДГОТОВКА К ОГЭ – 2016
Задание № 16 МОУ «Лицей № 47» Ленинского района г. Саратова Провоторова А.В. 2016 год

Задание № 16 (спецификация)
Умение исполнить алгоритм, записанный на естественном языке, обрабатывающий цепочки символов или списки. Уровень сложности задания – повышенный; Максимальный балл за выполнение задания – 1; Примерное время выполнения задания (мин) - 7

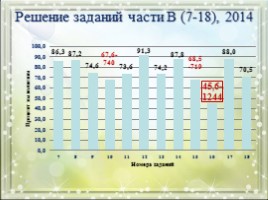
Решение заданий части В (7-18), 2014

Задание 16 (демо-версия 2016)
Автомат получает на вход трёхзначное десятичное число. По полученному числу строится новое десятичное число по следующим правилам. 1. Вычисляются два числа – сумма старшего и среднего разрядов, а также сумма среднего и младшего разрядов заданного числа. 2. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей). Пример. Исходное число: 277. Поразрядные суммы: 9, 14. Результат: 149. Определите, сколько из приведённых ниже чисел могут получиться в результате работы автомата. 1616 169 163 1916 1619 316 916 116 В ответе запишите только количество чисел. Ответ: ___________________________.

Решение:
Устанавливаем границы, в рамках которых будут находиться наши числа: min 100 max 999 Далее начинаем рассматривать каждое число из условия: 1616 – подходит, так как число может быть 888; 169 - подходит, так как число может быть 881; 163 – не подходит, так как первая сумма цифр и вторая не получаются в результате сложения; 1916 – 19 – первая пара не может быть, так как максимальное число при сумме составляет 18; 1619 – данное число представлено в порядке возрастания, а это противоречит условию; 316 - данное число представлено в порядке возрастания, а это противоречит условию; 916 - данное число представлено в порядке возрастания, а это противоречит условию; 116 - подходит, так как число может быть 560. ОТВЕТ: 3.

Решение подобного задания с сайта Полякова К.Ю. http://kpolyakov.spb.ru/
Тема: Выполнение и анализ простых алгоритмов. Что нужно знать: в общем-то, никаких знаний из курса информатики здесь не требуется, эту задачу можно давать детям начальной школы для развития логического мышления

http://kpolyakov.spb.ru/
Р-06. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам. 1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа. 2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей). Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114. Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

http://kpolyakov.spb.ru/ Решение:
единственный способ разбить запись 1311 на два числа – это 13 и 11 (числа 131 и 311 не могут образоваться в результате сложения значений двух десятичных цифр) сумма первой и второй цифр должна быть наименьшей (тогда и число будет меньше!), она равна 11; тогда сумма значений двух последних цифр равна 13 для того, чтобы всё число было минимально, числа, составленные из первых двух и последних двух цифр должны быть минимальными соответственно для сумм 11 и 13 минимальное двузначное число, у которого сумма значений цифр равна 11, - это 29, с этих двух цифр начинается исходное четырёхзначное число сумма двух последних цифр – 13, минимальное двузначное число с такой суммой цифр – 49. Ответ: 2949.

http://kpolyakov.spb.ru/
Р-02. Автомат получает на вход два трехзначных числа. По этим числам строится новое число по следующим правилам. Вычисляются три числа – сумма старших разрядов заданных трехзначных чисел, сумма средних разрядов этих чисел, сумма младших разрядов. Полученные три числа записываются друг за другом в порядке убывания (без разделителей). Пример. Исходные трехзначные числа: 835, 196. Поразрядные суммы: 9, 12, 11. Результат: 12119 Определите, какое из следующих чисел может быть результатом работы автомата. 1) 151303 2) 161410 3) 191615 4) 121613

http://kpolyakov.spb.ru/ Решение:
итак, число строится из трех чисел, каждое из которых может быть однозначным (от 0 до 9) или двузначным (от 10 до 9 + 9 = 18) если в числе 6 цифр, значит соединены три двузначных числа; в первом числе одно из них записывается как «03», что недопустимо (в этом случае правильное число было бы записано как 15133) в третьем числе тоже 6 цифр: три двузначных числа, первое из которых равно 19, чего не может быть (никакие два однозначных числа не могут дать такую сумму) в четвертом числе тоже 6 цифр: три числа 12, 16 и 13 расположены НЕ в порядке убывания, поэтому этот вариант неверен во втором варианте никаких противоречий с условием нет таким образом, ответ: 2.

Задание с сайта inf.сдамгиа.рф
Автомат получает на вход четырёхзначное десятичное число. По полученному числу строится новое десятичное число по следующим правилам. Вычисляются два числа — сумма первой и второй цифр и сумма третьей и четвёртой цифр заданного числа. 2. Полученные два числа записываются друг за другом в порядке невозрастания (без разделителей). Пример. Исходное число: 2177. Поразрядные суммы: 3, 14. Результат: 143. Определите, сколько из приведённых ниже чисел могут получиться в результате работы автомата. 1915 10 110 1516 1211 316 1519 116 1515 В ответе запишите только количество чисел.

Решение с сайта inf.сдамгиа.рф
Проанализируем каждое число. Число 1915 не может быть результатом работы автомата, поскольку невозможно получить число 19 как сумму цифр десятичного числа. Число 10 может быть результатом работы автомата, в этом случае исходное число могло быть 1000. Число 110 может быть результатом работы автомата, в этом случае исходное число могло быть 5600. Число 1516 не может быть результатом работы автомата, поскольку числа 15 и 16 расположены в порядке возрастания, а число 151 не может быть получено как сумма цифр десятичного числа. Число 1211 может быть результатом работы автомата, в этом случае исходное число могло быть было 6656. Число 316 не может быть результатом работы автомата, поскольку невозможно получить числа 3 и 16 расположены в порядке возрастания, а число 31 не может быть получено как сумма цифр десятичного числа. Число 1519 не может быть результатом работы автомата, поскольку невозможно получить число 151 как сумму цифр десятичного числа. Число 116 может быть результатом работы автомата, в этом случае исходное число могло быть 5633. Число 1515 может быть результатом работы автомата, в этом случае исходное число могло быть 7878. Таким образом, имеем пять чисел, которые могут являться результатом работы автомата. Ответ: 5. Источник: МИОО: Диагностическая работа по информатике 06.03.2014 вариант ИН90701.

http://kpolyakov.spb.ru/
Р-00. Цепочка из трех бусин, помеченных латинскими буквами, формируется по следующему правилу. В конце цепочки стоит одна из бусин A, B, C. На первом месте – одна из бусин B, D, C, которой нет на третьем месте. В середине – одна из бусин А, C, E, B, не стоящая на первом месте. Какая из перечисленных цепочек создана по этому правилу? 1) CBB 2) EAC 3)BCD 4) BCB

http://kpolyakov.spb.ru/ Решение (краткое):
проверяем первое условие: «В конце цепочки стоит одна из бусин A, B, C». Ему не удовлетворяет цепочка BCD, ее можно вычеркнуть: 1) CBB 2) EAC 3)BCD 4) BCB проверяем второе условие: «На первом месте – одна из бусин B, D, C, которой нет на третьем месте». Ему не удовлетворяют цепочки EAC (на первом месте – E) и BCB (на первом и третьем местах стоит буква B), поэтому остается только вариант CBB: 1) CBB 2) EAC 4) BCB проверяем третье условие: «В середине – одна из бусин А, C, E, B, не стоящая на первом месте». К счастью, оставшаяся цепочка CBB ему удовлетворяет. таким образом, правильный ответ – 1. Возможные проблемы: не все могут сделать подобный анализ в уме!!!

http://kpolyakov.spb.ru/ Решение (подробный вариант ):
Правило содержит три условия, обозначим их так: У1: третья бусина – A, B или C У2-3: первая бусина – B, D или C, не совпадающая с третьей У4-5: вторая бусина – A, B, C или E, не совпадающая с первой фактически условия У2-3 и У4-5 сложные, их можно разбить на два, так что получится всего пять условий У1: третья бусина – A, B или C У2: первая бусина – B, D или C У3: первая и третья бусины – разные У4: вторая бусина – A, B, C или E У5: первая и вторая бусины – разные. Теперь для каждого из ответов проверим выполнение всех условий; в таблице крестик обозначает, что условие не выполняется для данного варианта; зеленым цветом выделена строка, где нет ни одного крестика, то есть все условия выполняются. Таким образом, правильный ответ – 1.
У1 У2 У3 У4 У5
1) CBB
2) EAC 
3) BCD 
4) BCB 

Задание с сайта inf.сдамгиа.рф
Цепочка из трёх бусин, помеченных латинскими буквами, формируется по следующему правилу: –в середине цепочки стоит одна из бусин C, E, D, A; – в конце – одна из бусин H, A, C, которой нет на втором месте; – на первом месте – одна из бусин H, A, E, D, не стоящая в конце. Определите, сколько из перечисленных цепочек созданы по этому правилу? HCA AEA DAH ECC EEH ADE CEA AED EHA В ответе запишите только количество цепочек.

Решение с сайта inf.сдамгиа.рф
Первому условию правила не соответствует последняя цепочка EHA. Второму условию не соответствует предпоследняя цепочка AED, ADE и ECC. Третьему правилу не соответствуют цепочки AEA и CEA. Таким образом, три цепочки (HCA, DAH и EEH) сформированы по предложенному правилу. Ответ: 3. Источник: СтатГрад: Тренировочная работа по информатике 23.03.15 вариант ИН90601.

Задание с сайта inf.сдамгиа.рф
Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если она нечётна, то удаляется первый символ цепочки, а если чётна, то в середину цепочки добавляется символ А. В полученной цепочке символов каждая буква заменяется буквой, следующей за ней в русском алфавите (А — на Б, Б — на В и т. д., а Я — на А). Получившаяся таким образом цепочка является результатом работы алгоритма. Например, если исходной была цепочка РУКА, то результатом работы алгоритма будет цепочка СФБЛБ, а если исходной была цепочка СОН, то результатом работы алгоритма будет цепочка ПО. Дана цепочка символов БРА. Какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т. е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)? Русский алфавит: АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.

Решение с сайта inf.сдамгиа.рф
Применим алгоритм: БРА (нечётное) → РА → СБ. Применим его ещё раз: СБ (чётное) → САБ → ТБВ. Ответ: ТБВ Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1301.

Спасибо за внимание!

источник шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново Сайт: http://pedsovet.su/