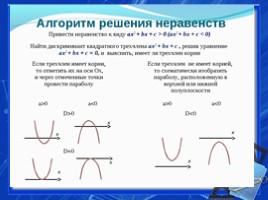
Презентация - Решение неравенств второй степени с одной переменной
Примеры похожих презентаций
 Технологическая карта урока алгебры в 8-м классе «Решение систем неравенств с одной переменной»
Технологическая карта урока алгебры в 8-м классе «Решение систем неравенств с одной переменной» Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Решение систем уравнений второй степени урок закрепления знаний. Борисова в.С. Учитель математики мбоу сош №11
Решение систем уравнений второй степени урок закрепления знаний. Борисова в.С. Учитель математики мбоу сош №11 Решение систем уравнений второй степени
Решение систем уравнений второй степени Решение неполного уравнения третьей степени
Решение неполного уравнения третьей степени По наличию второстепенных членов. Нераспространенные. Распространенные
По наличию второстепенных членов. Нераспространенные. Распространенные Главные и второстепенные члены предложения
Главные и второстепенные члены предложения
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.