Презентация - Решение задач с помощью квадратных уравнений

Решение задач с помощью квадратных уравнений
Необходимость решать квадратные уравнения еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения вавилоняне умели решать еще около 2000 лет до н. э. правило решения этих уравнений, изложенное в Вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила.
(c) Коробейникова Н.А.
1
материал подготовлен для сайта matematika.ucoz.com

Диофант (ок.3 в.дон.э.)
древнегреческий математик из Александрии
Он собирал известные и придумывал новые задачи, а позднее объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть пережили хаос Средних веков и стали источником вдохновения для математиков эпохи Возрождения. Остальные семь книг погибли в результате цепочки трагических событий, которые отбросили математику к временам древних вавилонян.
В верхней строке записано уравнение
Лист из Арифметики
(c) Коробейникова Н.А.
материал подготовлен для сайта matematika.ucoz.com

Фибоначчи-1170г
Формулы решения квадратных уравнений в Европе были впервые изложены в”Книге об абаке”, написанной в 1202 году итальянским математиком Леонардо Фибоначчи. Его книга способствовала распространению алгебраических знаний не только в Италии, но и Германии, Франции и других странах Европы.
(c) Коробейникова Н.А.
3
материал подготовлен для сайта matematika.ucoz.com

Этот вывод и был сформулирован впервые французским математиком Франсуа Виетом, который все знают как теорема Виета
В приведенном квадратном уравнении сумма корней уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение его корней равно свободному коэффициенту x1 + x2 = –p x1 • x2 = q
(c) Коробейникова Н.А.
4
материал подготовлен для сайта matematika.ucoz.com

Но общее правило решения квадратных уравнений, при всевозможных комбинациях коэффициентов b и c было сформулировано в Европе лишь в 1544 году немецким математиком М.Штифелем.
М.Штифель
(c) Коробейникова Н.А.
5
материал подготовлен для сайта matematika.ucoz.com

Спортивная площадка площадью 1800кв.м имеет форму прямоугольника, длина которого на 5м больше ширины. Найдите размеры площадки.
задача1
(c) Коробейникова Н.А.
6
материал подготовлен для сайта matematika.ucoz.com

решение
Пусть Xм ширина площадки;
(x+5)м длина площадки.
По условию задачи площадь спортивной площадки равна 1800м2 .
Составим уравнение.
x(x+5)=1800,
x2+5x-1800=0,
D=25+7200=7225,
X1=-45 (не удовлетворяет условию задачи),
X2=40 (м) – ширина участка .
40+5=45(м) – длина участка.
Ответ. 40м и 45м.
(c) Коробейникова Н.А.
7
материал подготовлен для сайта matematika.ucoz.com

Найти два последовательных натуральных числа, произведение которых равно 132.
Задача2
Справка. Натуральные числа: 1,2,3,4,5,6,7,…
(c) Коробейникова Н.А.
8
материал подготовлен для сайта matematika.ucoz.com

задача3
Найти два последовательных нечетных числа, если их произведение равно 195.
Справка. Нечетные числа: 1,3,5,7,9,11,..
(c) Коробейникова Н.А.
9
материал подготовлен для сайта matematika.ucoz.com

задача4
Периметр прямоугольника равен 10 м, площадь-6 кв. м. Найти его стороны.
(c) Коробейникова Н.А.
10
материал подготовлен для сайта matematika.ucoz.com

Задача5.Индусская задача
«На две партии разбившись, Забавлялись обезьяны. Часть восьмая их в квадрате В роще весело резвилась Криком радостным двенадцать Воздух свежий оглашали... Вместе сколько ты мне скажешь, Обезьян там было в роще?»
(c) Коробейникова Н.А.
11
материал подготовлен для сайта matematika.ucoz.com

решение
Задача имеет два решения
(c) Коробейникова Н.А.
12
материал подготовлен для сайта matematika.ucoz.com

Задача 6
Определите стороны прямоугольного поля площадью 140 га, если одна его сторона на 400 м больше другой.
Справка 1га-10000кв.м
(c) Коробейникова Н.А.
13
материал подготовлен для сайта matematika.ucoz.com

решение
хм – сторона поля; (х+400)м- другая сторона. По условию площадь 1400000кв.м. Составим уравнение. х(х+400)=1400 000,
D=5760000,
х1=1000, х2=1400.
Ответ. 1000м, 1400м.
(c) Коробейникова Н.А.
14
материал подготовлен для сайта matematika.ucoz.com

задача6
Расстояние между городами скорый поезд, идущий со скоростью  90 км/ч, проходит на 1,5 ч быстрее товарного, который идет со скоростью 60 км/ч. Каково расстояние между городами?
(c) Коробейникова Н.А.
15
материал подготовлен для сайта matematika.ucoz.com

решение
Х км/ч-расстояние между городами; х/90 ч-время скорого поезда; х/60 ч-время товарного поезда; х/90 меньше х/60 на 1,5часа. Составим уравнение: х/60  - х/90 = 3/2; 3х-2х=270; Х=270. Ответ. 270 км.
(c) Коробейникова Н.А.
16
материал подготовлен для сайта matematika.ucoz.com

Задача7
Ученику и мастеру дано задание изготовить одинаковое количество деталей. Мастер, изготовляя 18 деталей в час, затратил на выполнение задания на 3 ч меньше, чем ученик, который изготавливал лишь 12 деталей в час. Сколько деталей было заказано?
(c) Коробейникова Н.А.
17
материал подготовлен для сайта matematika.ucoz.com

Решение.
Х-вся работа; х/18 ч.- время затраченное мастером; х/12 ч.- время затраченное учеником; х/18 меньше х/12 на 3 часа. Составим уравнение: х/12 – х/18 = 3; 3х-2х=108; Х=108. Ответ.108 деталей.
(c) Коробейникова Н.А.
18
материал подготовлен для сайта matematika.ucoz.com

задача8
Автобус-экспресс отправился от вокзала в аэропорт, находящийся на расстоянии 60км от вокзала. Пассажир, опоздавший на 5 минут на автобус, решил добраться до аэропорта на такси. Скорость такси на 10км/ч больше скорости автобуса. С какой скорость ехал автобус, если он приехал в аэропорт одновременно с такси? 
(c) Коробейникова Н.А.
19
материал подготовлен для сайта matematika.ucoz.com

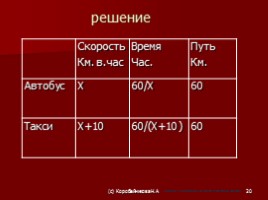
решение
Скорость Км. в.час Время Час. Путь Км.
Автобус Х 60/Х 60
Такси Х+10 60/(Х+10 ) 60
(c) Коробейникова Н.А.
20
материал подготовлен для сайта matematika.ucoz.com

60/(Х+10) меньше 60/Х на1/12. Составим уравнение: 60/Х -60/(Х+10)=1/12; 720(х+10 )-720х=х(х+10); 720х+7200-720х= х²+10х; х²+10х-7200=0; Д=28900; x1=-90 не удовлетворяет условию; X2=80. Ответ. 80 км.в час.
(c) Коробейникова Н.А.
21
материал подготовлен для сайта matematika.ucoz.com

Задача 9
Для вывоза песка из карьера в автопарке было заказано несколько одинаковых грузовых автомобилей. Руководство автопарка решило, что на каждую машину можно погрузить на одну тонну груза больше, чем рассчитывали, и поэтому прислало на 4 машины меньше. В итоге все 80 тонн песка были вывезены. Сколько машин было заказано в автопарке? 
(c) Коробейникова Н.А.
22
материал подготовлен для сайта matematika.ucoz.com

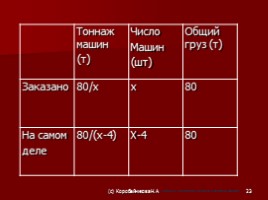
Тоннаж машин (т) Число Машин (шт) Общий груз (т)
Заказано 80/х х 80
На самом деле 80/(х-4) Х-4 80
(c) Коробейникова Н.А.
23
материал подготовлен для сайта matematika.ucoz.com

=
80/(х-4) больше 80/х на 1 тонну. Составим уравнение: 80/(х-4)-80/х=1; 80х-80х+320 = х²-4х; х²-4х-320=0; Д=1296; x1=-16 НЕ УДОВЛЕТВОРЯЕТ УСЛОВИЮ; X2=20. Ответ. 20 машин.
(c) Коробейникова Н.А.
24
материал подготовлен для сайта matematika.ucoz.com

1. Ученик решил прочитать книгу, содержащую 480 страниц, за несколько дней. Но каждый день он читал на 20 страниц больше, чем предполагал, и поэтому прочитал книгу на 4 дня раньше. За сколько дней была прочитана книга? 2.Теплоход прошёл 18 км по озеру и 40 км по течению реки за 2 ч. Найдите скорость теплохода при движении по озеру, если скорость течения реки равна 3 км/ч.   3.Расстояние между городами скорый поезд, идущий со скоростью  90 км/ч, проходит на 1,5 ч быстрее товарного, который идет со скоростью 60 км/ч. Каково расстояние между городами?
(c) Коробейникова Н.А.
25
материал подготовлен для сайта matematika.ucoz.com

ответы
1.(480/(х-4) – 480/х = 20; х = 12) 2. (18/х + 40/(х+3) = 2, х = 27) 3. (270км.)
(c) Коробейникова Н.А.
26
материал подготовлен для сайта matematika.ucoz.com