Презентация - Симметрия для 7 класса

Симметрия
Бабаева Алексея 7”Б”

Содержание
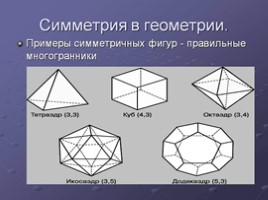
Симметрия Виды симметрии Другие названия Симметрия листьев Животные Симметрия в геометрии Симметрия снежинок

Симметрия в широком смысле — неизменность при каких-либо преобразованиях.
В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, одинаковость в расположении частей».

Зеркальная и лучевая симметрия
Симметрия широко встречается в объектах живой и неживой природы. Установлено, что в природе наиболее распространеныдва вида симметрии - "зеркальная" и "лучевая" (или "радиальная") симметрии.

Другие названия
Зеркальная симметрия еще называется "симметрией листка" или "билатеральной симметрией" . Часто лучевой вид симметрии называется "ромашко-грибной" симметрией.

Все то, что растет или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой ("ромашко-грибной") симметрии. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется блатеральной симметрии - "симметрии листка" (одна плоскость симметрии)".

.
Математики вкладывают в понятие симметрия точный математический смысл, рассматривают специальные виды симметрии. И в результате симметрия становится мощным средством математических исследований, помогает решать трудные задачи.

Симметрия листьев

Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. В пространстве существуют тела, обладающие винтовой симметрией, т. е. совмещающиеся со своим первоначальным положением   после   поворота   на угол   вокруг  оси,   дополненного сдвигом вдоль той же оси. Винтовая симметрия наблюдается  в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений.

Животные

Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила. Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, такие как  радиальную (лучевая) или билатеральную (двусторонняя), которые являются основными типами симметрии. Кстати, склонность  к регенерации (восстановление) зависит от типа симметрии животного

Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много – любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник.

Симметрия в снежинках

Ещё более ярко и систематически симметричность структуры материи обнаруживается в неживой природе, а именно в кристаллах. При слове «кристалл» в воображении рисуется первый среди драгоценных камней – алмаз: «кристальная» чистота и прозрачность, чудесная, непередаваемая игра света, идеальная, правильная форма. Но теперь алмазы не только предмет роскоши. Сегодня они служат для обработки наиболее твёрдых металлов и сплавов. Без них не мыслится современная металлообрабатывающая промышленность. Оказывается, не только алмаз кристалл. Обычный сахар и поваренная соль, лёд и песок состоят из множества кристалликов. Больше того, основная масса горных пород, образующих земную кору, состоит из кристаллов. Даже обыкновенная глина представляет собой нагромождение мельчайших кристалликов. Словом, большинство строительных материалов – металлы, камень, песок, глина – кристаллические вещества. Можно сказать, что  мы живём  в домах, построенных из кристаллов. Неудивительно, что кристаллы являются предметом тщательного изучения

Заключение
Хотелось бы сказать, что почти во всём, что нас окружает, есть та или иная симметрия. О ней можно говорить бесконечно. Поэтому, заканчивая свой проект, я надеюсь, что смог передать сложность и привлекательность этой темы. И могу с уверенностью также сказать, что составляющие основу красоты природы явления симметрии и периодичности хорошо изучены и описаны математически.

Спасибо за внимание!