Презентация - Дельтоид для 9 класса

Дельтоид
Выполнили: обучающиеся 8 «А» класса ГБОУ школы-интерната №113 г.о. Самара Елдышева Дарья, Левчук Станислав, Шапкина Алина Руководитель: Губарева Е.Г.

Цель: изучить четырехугольник «Дельтоид», описать его свойства и признаки, составить учебное пособие.
Задачи: Изучить и проанализировать литературу по данной теме. Сформулировать и доказать свойства и признаки дельтоида. Составить и решить задачи о дельтоиде. Продемонстрировать наличие дельтоидов в окружающем нас мире. Составить тест проверки знаний о дельтоидах.

Основные понятия
Дельтоид — четырехугольник, у которого есть две пары смежных сторон. Равными являются две пары смежных сторон. Дельтоид имеет форму, похожую на воздушного змея.

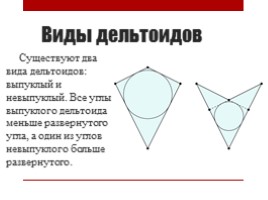
Виды дельтоидов
Существуют два вида дельтоидов: выпуклый и невыпуклый. Все углы выпуклого дельтоида меньше развернутого угла, а один из углов невыпуклого больше развернутого.

Свойство 1.
Углы дельтоида между сторонами неравной длины равны. Дано: АВСD — дельтоид, ВD — главная диагональ. Доказать: ∠А = ∠С.

Рассмотрим треугольники АВС и АDC. У них сторона АС – общая. Стороны АВ = АD, ВС = СD по условию. Значит, треугольники равны по третьему признаку равенства треугольников. Следовательно ﮮАВС = ﮮАDС. Что и требовалось доказать.
Доказательство свойства 1.

Свойство 2.
Главная диагональ дельтоида является биссектрисой противолежащих углов. Дано: АВСD - дельтоид, BD — главная диагональ. Доказать: BD - биссектриса.

Из доказательства свойства1 следует, что ∆ АВС = ∆ АDС. Значит ﮮВАС = ﮮDАС, ﮮВСА = ﮮDСА. Вывод: АС – биссектриса, что и требовалось доказать.
Доказательство свойства 2.

Свойство 3.
Диагонали дельтоида (или их продолжения) пересекаются под прямым углом, одна из них делит другую на равные части.

Рассмотрим ∆ АВС. Он является равнобедренным по условию. Из этого следует, что биссектриса ﮮВ, проведенная к основанию треугольника, является еще высотой и медианой. Следовательно, ОА = ОС, а диагонали ВD ┴ АС одна из них делится точкой пересечения пополам. Что и требовалось доказать.
Доказательство свойства 3.

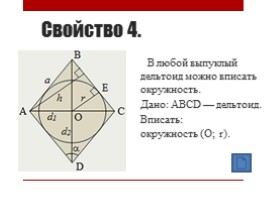
Свойство 4.
В любой выпуклый дельтоид можно вписать окружность. Дано: АВСD — дельтоид. Вписать: окружность (О; r).

Доказательство свойства 4.
Известно, что если суммы длин противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (т.к. АВ = СВ и АD = DС, то АВ + DС = СВ + АD). По определению дельтоида, это выпуклый четырехугольник, у которого есть только две пары смежных сторон. Значит АВ +DС = АD + ВС. Точка О пересечение биссектрис СО и АО углов С и А. Следовательно: в дельтоид можно вписать окружность и притом только одну. Что и требовалось доказать.

Свойство 5.
Средние линии дельтоида образуют прямоугольник, периметр которого равен сумме диагоналей данного дельтоида. Дано: АВСD — дельтоид, L, E, F, M - середины сторон. Доказать: MLEF - прямоугольник.

Доказательство свойства 5.
MF║BD и LE ║DB, т.е. MF ║LE ML ║CA и EF ║CA, т.е. ML ║ EF CA ┴ BD, значит и ML и EF ┴ MF и LE, отсюда следует, что ﮮМ = ﮮL, ﮮЕ = ﮮF, и ML + EF = CA и MF + LE = BD. Следует, что периметр = ML + EF + MF +LE = = CA + BD. Что и требовалось доказать.

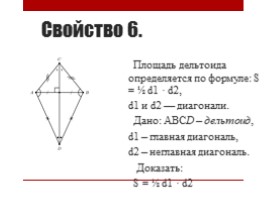
Свойство 6.
Площадь дельтоида определяется по формуле: S = ½ d1 · d2, d1 и d2 — диагонали. Дано: АВСD – дельтоид, d1 – главная диагональ, d2 – неглавная диагональ. Доказать: S = ½ d1 · d2

Доказательство свойства 6.
Рассмотрим ∆ АDC, он равнобедренный, ОD – высота. Площадь равна высоте умноженной на половину основания. S (ADC) = 0,5∙ DO∙ d2. Рассмотрим ∆ BCA - равнобедренный, ОB - высота. S (BCA) = 0,5∙ BO∙ d2. S (ABCD) = S (ADC) + S (BCA) = 0,5∙ DO∙ d2 + +0,5∙ BO∙ d2 = 0,5∙d1∙d2. Что и требовалось доказать.

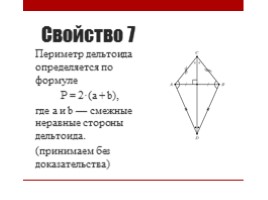
Свойство 7
Периметр дельтоида определяется по формуле Р = 2·(а + b), где a и b — смежные неравные стороны дельтоида. (принимаем без доказательства)

Свойство 8
Не главная диагональ делит дельтоид на два равнобедренных треугольника. Дано: АВСD -дельтоид. Доказательство: по определению дельтоида очевидно, что ∆ АВD и ∆ВСD равнобедренные.

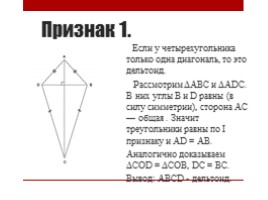
Признак 1.
Если у четырехугольника только одна диагональ, то это дельтоид. Рассмотрим ΔАВС и ΔАDС. В них углы В и D равны (в силу симметрии), сторона АС — общая . Значит треугольники равны по I признаку и АD = АВ. Аналогично доказываем ΔСОD = ΔСОВ, DС = ВС. Вывод: АВСD - дельтоид.

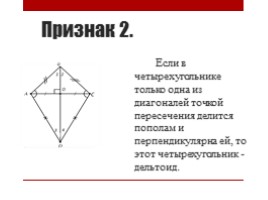
Признак 2.
Если в четырехугольнике только одна из диагоналей точкой пересечения делится пополам и перпендикулярна ей, то этот четырехугольник - дельтоид.

Доказательство признака 2.
Дано: четырехугольник АВСD, d1 ┴ d2, AO = OC. Доказать: АВСD – дельтоид. Док-во: 1. Рассмотрим ∆ АОD, АВ входит в ∆ АОВ и АО ┴ DВ. 2. Рассмотрим ∆ АОD и ∆ АОВ: АО – общая, ﮮ1 = ﮮ2 ∆ АОD = ∆ АОВ, по катету и противолежащему углу, отсюда АD = АВ. 3. DС входит в ∆ СОD и СО ┴ DВ. 4. Рассмотрим ∆ СОD и ∆ СОВ: ОС – общая, ﮮ3 = ﮮ4 ∆ СОD = ∆ СОВ, по катету и прилежащему острому углу, отсюда DС = ВС.

Доказательство признака 2.
5. Биссектриса равнобедренного треугольника, проведенная из вершины равнобедренного треугольника, является медианой и высотой, т.е. АО и СО – медианы, значит DO = OB. 6. DO – перпендикуляр, не является медианой, т.к. ∆ ADC не равнобедренный. Значит ABDC – дельтоид по определению. Что и требовалось доказать.

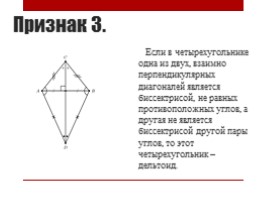
Признак 3.
Если в четырехугольнике одна из двух, взаимно перпендикулярных диагоналей является биссектрисой, не равных противоположных углов, а другая не является биссектрисой другой пары углов, то этот четырехугольник – дельтоид.

Доказательство признака 3.
Дано : четырехугольник АВСD, d1 –биссектриса (ﮮ,1 = 2), ﮮ d2 – не является биссектрисой, d1 ┴ d2. Доказать: АВСD – дельтоид. Док-ть: АВ входит в ∆ АОВ и АО ┴ DВ. 2. Рассмотрим ∆ АОD и ∆ АОВ: АО – общая. ﮮ 1 = ﮮ2. т.к. d1 –биссектриса по условию, ∆ АОD = ∆ АОВ, по катету и противолежащему углу, отсюда АD = АВ. 3. DС входит в ∆ СОD и СО ┴ DВ.

Задача 1
Найдите периметр дельтоида ABCD, если известно, что : периметр ∆ABD, входящего в состав дельтоида равен 30см. Диагональ BD = 18см. Отрезок ОС = 2см.
Решение: периметр ∆ ABD = 21см. АВ + АD 30 – 18 = 12. По теореме Пифагора: АС = 15 (9² + 12² = 15²). Р (АВСD) = 6 + 6 + 15 + 15 = 66. Ответ: Р(АВСD) = 66см.

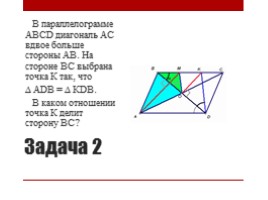
Задача 2
В параллелограмме АВСD диагональ АС вдвое больше стороны АВ. На стороне ВС выбрана точка К так, что ∆ АDВ = ∆ КDВ. В каком отношении точка К делит сторону ВС?

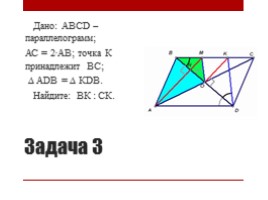
Задача 3
Дано: АВСD – параллелограмм; АС = 2∙АВ; точка К принадлежит ВС; ∆ АDВ = ∆ КDВ. Найдите: ВК : СК.

Решение задачи 2.
Дано: АВСD – параллелограмм; АС = 2АВ; точка К принадлежит ВС; ∆ АDВ = ∆ КDВ. Найти: ВК/СК. Решение: 1. Пусть О – точка пересечения диагоналей АС и ВD. Т.к. ∆ АDВ = ∆ КDВ, то ВК = DК , т.е. КО – высота равнобедренного треугольника ВКD. 2. АО = АВ. Проведем высоту АN равнобедренного ∆ВАО и продолжим ее до пересечения с прямой ВС в точке М. Т.к. N – середина ВО и МN║КО, ВМ = ВК ( по теореме Фалеса). Аналогично О – середина АС и ОК║АМ, то МК = КС. Следовательно, ВК КС = 2 1 .

История изучения дельтоида
Дельтоида (кривая Штейнера) — плоская алгебраическая кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой в 3 раза больше радиуса первой.

Дельтоид в окружающем нас мире.

Дельтоидом называют мышцы плеча
Человеческий мозжечок имеет рисунок, который ученые называют (деревом жизни), составной частью которого являются дельтоиды.

Тест « Знаешь ли ты дельтоид?»
Вопрос 1 Выберите верное утверждение. Если в четырехугольнике главная диагональ – биссектриса противоположных углов, то это дельтоид; Если в четырехугольнике две стороны равны, то это дельтоид; Если в четырехугольнике есть пара смежных сторон, то это дельтоид; Если четырехугольник образован двумя равнобедренными треугольниками, то это дельтоид.

Тест « Знаешь ли ты дельтоид?»
Вопрос 2. В дельтоиде смежные стороны относятся как 2 : 3. Найдите меньшую сторону, если периметр дельтоида равен 60 см. 6 12 9 10.

Тест « Знаешь ли ты дельтоид?»
Вопрос 3. Выбери четырехугольник, который может быть выпуклым: Трапеция Ромб Дельтоид Квадрат

Тест « Знаешь ли ты дельтоид?»
Вопрос 4. Как называется четырехугольник, у которого только одна диагональ является биссектрисой противолежащих углов? Трапеция Дельтоид Ромб Прямоугольник

Тест « Знаешь ли ты дельтоид?»
Вопрос 5. АВСD – дельтоид. Площадь ∆АВС = 45. Площадь ∆ АСD = 55. ∆АВС равносторонний, ∆АСD – равнобедренный. Найдите площадь дельтоида, 60 50 55 100

Тест « Знаешь ли ты дельтоид?»
Вопрос 6. Выбери верные утверждения: Средняя линия дельтоида – это линия, соединяющая стороны дельтоида; Главная диагональ дельтоида – это диагональ, соединяющая вершины неравных углов дельтоида; Дельтоид – четырехугольник, в котором две пары смежных сторон равны; Неглавной диагональю дельтоида называется диагональ, соединяющая две его вершины.

Тест « Знаешь ли ты дельтоид?»
Вопрос 7. Выберите определение дельтоида: Дельтоид – это четырехугольник, у которого стороны попарно равны; Дельтоид – это четырехугольник, у которого смежные стороны попарно равны; Дельтоид – это четырехугольник, у которого у которого диагонали взаимно перпендикулярны; Дельтоид – это четырехугольник, у которого две стороны равны и параллельны;

Тест « Знаешь ли ты дельтоид?»
Вопрос 8. Какого из перечисленных элементов нет у дельтоида? угол; Диагональ; Радиус вписанной окружности; Радиус описанной окружности.

Спасибо за внимание