Презентация - Квадратное уравнение и его корни

«Если действовать не будешь, ни к чему ума палата»…
Ш. Руставели

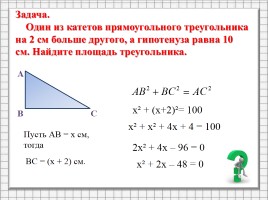
х² + (х+2)²= 100
Задача. Один из катетов прямоугольного треугольника на 2 см больше другого, а гипотенуза равна 10 см. Найдите площадь треугольника.
Пусть АВ = х см, тогда
ВС = (х + 2) см.
х² + х² + 4х + 4 = 100
2х² + 4х – 96 = 0
х² + 2х – 48 = 0
А
В
С

A) 2х² +3х = 4
B) 4х – 8 = х + 5
K) 2х + 5 = -7
C) х² - 3х – 5 = 0
D) 2(х – 3) = 6х + 7
E) (х + 4) – 3(2х – 1) = 1
F) х² +7х = 0
M) 5х(х – 1) = 2

Квадратное уравнение и его корни.

Цели урока:
Ввести определение квадратного уравнения Научиться определять по внешнему виду квадратные уравнения Уметь определять значения коэффициентов квадратного уравнения Научиться решать простейшие квадратные уравнения

Квадратным уравнением называется уравнение вида ax² + bx + c =0, где a, b, c - заданные числа, а ≠ 0, х – неизвестное число
- х + 2x² - 3 =0
4x² - x = 0
3x² - x + 2 =0
- x² + 1 =0

а = 3 b= -1 с = 2
а = -1 b= 0 с = 1
а = 4 b= -1 с = 0
а = 2 b= -1 с = -3
Числа а, в, с – называются коэффициентами квадратного уравнения а - первый или старший коэффициент в – второй коэффициент с- свободный член

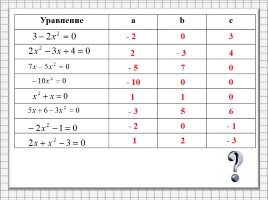
Укажите среди данных уравнений квадратные.

Укажите значения коэффициентов a,b,c квадратного уравнения.

Уравнение a b c
- 3
0
- 2
6
5
3
- 3
- 3
- 2
2
2
0
0
0
0
0
4
- 5
7
- 10
1
1
- 1
1

Оказывается, решать уравнения могли еще в глубокой древности. Вавилоняне умели решать квадратные уравнения около 2000 лет до н.э. Задачи на квадратные уравнения встречаются в астрономическом трактате написанном в 499г индийским математиком и астрономом. Другой индийский ученый в VIIв изложил общее правило решения квадратных уравнений. Древние греки решали квадратные уравнения графическим методом.

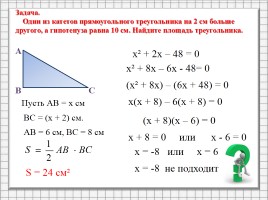
х² + 8х – 6х - 48= 0
Задача. Один из катетов прямоугольного треугольника на 2 см больше другого, а гипотенуза равна 10 см. Найдите площадь треугольника.
Пусть АВ = х см
ВС = (х + 2) см.
(х² + 8х) – (6х + 48) = 0
(х + 8)(х – 6) = 0
х² + 2х – 48 = 0
А
В
С
х(х + 8) – 6(х + 8) = 0
х + 8 = 0 или х - 6 = 0
х = -8 или х = 6
х = -8 не подходит
АВ = 6 см, ВС = 8 см
S = 24 см²

Пусть х м – длина забора
Квадратный участок, площадью 400 кв. м, огорожен забором. Найдите длину забора.
х = -20 – не подходит
Ответ:
длина забора 80 м.
х² м² - площадь участка
х² = 400
х² – 400 = 0
(х + 20)(х – 20) = 0
х + 20 = 0 или х – 20 = 0
х = -20 или х = 20
20 м – сторона участка
Р = 4 *20 = 80 (м) – периметр участка

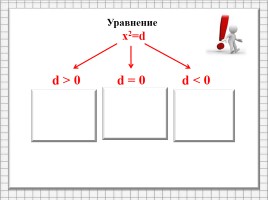
Уравнение х2=d
х=0
один корень
Нет корней
d > 0
d = 0
d < 0
два корня

Записать в один из столбцов таблицы каждое из уравнений:
Два корня
Один корень
Нет корней
1) х² = 16
2) х² = 20
3) х² = - 4
5) х² - 7 = 0
4)
6)
1
2
4
3
6
5

ОТВЕТЫ К ТЕСТУ
1 вариант А Б В Б Б
2 вариант Б В Б А В

Домашнее задание:
§ 25 № 403 – 404(нечетные), № 408 – 410(нечетные)
Дополнительно*: № 412, 414,415

Вопросы: Какую цель мы поставили в начале урока? Достигли ли вы цели? Какие этапы урока (виды деятельности) работали на достижение этих целей?

Спасибо за работу!