Слайды и текст этой онлайн презентации
Слайд 1
Методическая разработка Савченко Е.М.
МОУ гимназия №1, г. Полярные Зори, Мурманской обл.
Тетраэдр
параллелепипед
Геометрия 10
Слайд 2
A
В
D
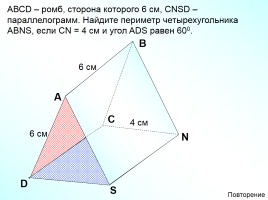
АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 600.
C
N
S
6 см
6 см
4 см
Повторение
Слайд 3
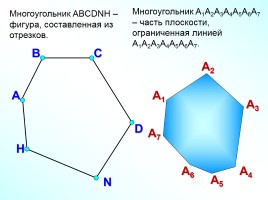
Многоугольник ABCDNH – фигура, составленная из отрезков.
А
В
С
D
H
N
Слайд 4
D
А
С
В
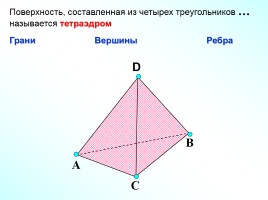
Поверхность, составленная из четырех треугольников …
называется тетраэдром
Грани Вершины Ребра
Слайд 6
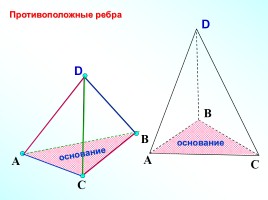
D
А
С
В
Противоположные ребра
основание
основание
Слайд 7
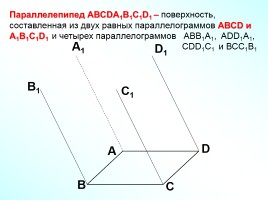
Параллелепипед АВСDA1B1C1D1 – поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1,
CDD1C1 и ВСС1В1
А
В
С
D
Слайд 8
А
В
С
D
D1
С1
A1
B1
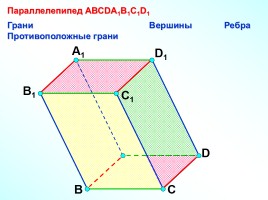
Параллелепипед АВСDA1B1C1D1
Грани Вершины Ребра
Противоположные грани
Слайд 10
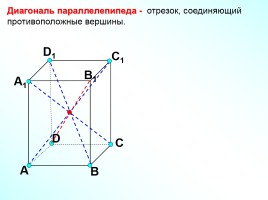
А
В
С
D
А1
D1
С1
B1
Диагональ параллелепипеда - отрезок, соединяющий противоположные вершины.
Слайд 11
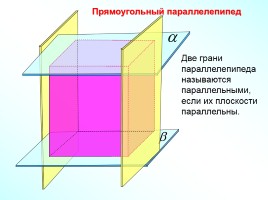
Прямоугольный параллелепипед
Две грани параллелепипеда называются параллельными, если их плоскости параллельны.
Слайд 12
А
В
С
D
D1
С1
A1
B1
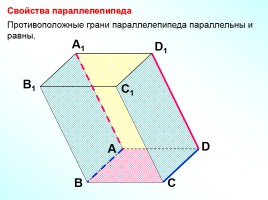
Свойства параллелепипеда
Противоположные грани параллелепипеда параллельны и равны.
Слайд 13
А
В
С
D
D1
С1
A1
B1
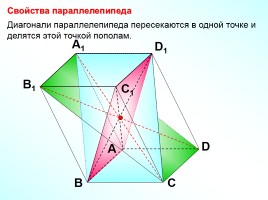
Свойства параллелепипеда
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Слайд 14
А
D
С
В
B1
С1
D1
А1
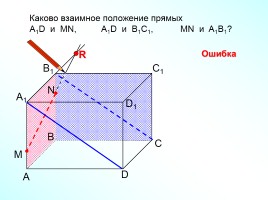
Каково взаимное положение прямых
А1D и MN, А1D и В1С1, МN и A1B1?
N
M
Ошибка
Слайд 15
А
D
С
В
B1
С1
D1
А1
F
E
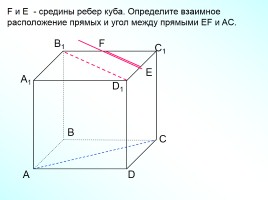
F и E - средины ребер куба. Определите взаимное
расположение прямых и угол между прямыми EF и AC.
Слайд 16
А
D
С
В
B1
С1
D1
А1
F
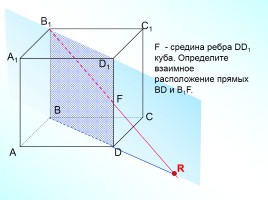
F - средина ребра DD1 куба. Определите взаимное
расположение прямых BD и B1F.
Слайд 17
А
D
С
В
B1
С1
D1
А1
F
E
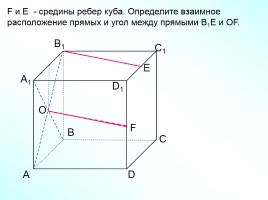
F и E - средины ребер куба. Определите взаимное
расположение прямых и угол между прямыми В1Е и ОF.
О
Слайд 18
А
D
С
В
B1
С1
D1
А1
F
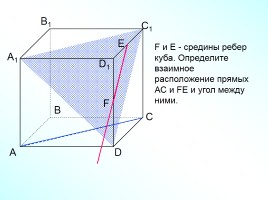
F и Е - средины ребер куба. Определите взаимное
расположение прямых АС и FЕ и угол между ними.
Е
Слайд 19
А
D
С
В
B1
С1
D1
А1
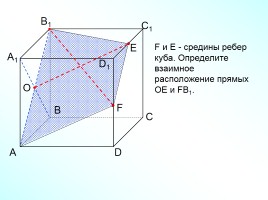
F
F и Е - средины ребер куба. Определите взаимное
расположение прямых ОЕ и FВ1.
Е
О
Слайд 20
А
В
С
D
N
M
E
F
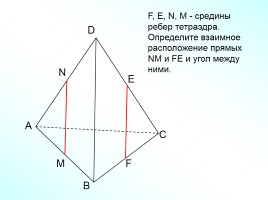
F, Е, N, M - средины ребер тетраэдра. Определите взаимное
расположение прямых NM и FЕ и угол между ними.
Слайд 21
А
В
С
D
N
M
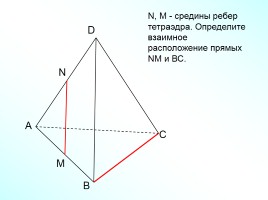
N, M - средины ребер тетраэдра. Определите взаимное
расположение прямых NM и ВС.
Слайд 22
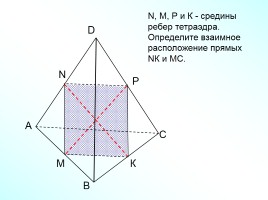
А
В
С
D
N
M
N, M, Р и К - средины ребер тетраэдра. Определите взаимное
расположение прямых NК и МС.
Р
К
Слайд 23
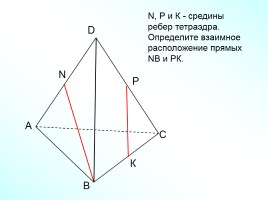
А
В
С
D
N
N, Р и К - средины ребер тетраэдра. Определите взаимное
расположение прямых NВ и РК.
Р
К
Слайд 24
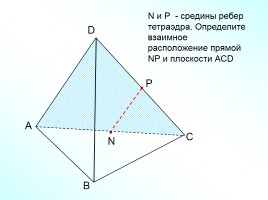
А
В
С
D
N
N и Р - средины ребер тетраэдра. Определите взаимное
расположение прямой NР и плоскости АСD
Р
Слайд 25
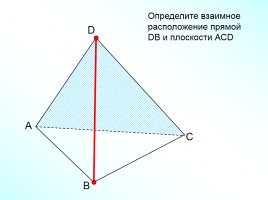
А
В
С
D
Определите взаимное
расположение прямой DВ и плоскости АСD
Слайд 26
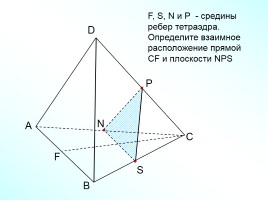
А
В
С
D
N
F, S, N и Р - средины ребер тетраэдра. Определите взаимное
расположение прямой CF и плоскости NPS
Р
S
F
Слайд 27
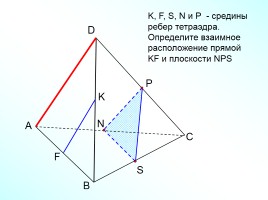
А
В
С
D
N
K, F, S, N и Р - средины ребер тетраэдра. Определите взаимное
расположение прямой KF и плоскости NPS
Р
S
F
K
 Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Прямоугольный параллелепипед (26,10)
Прямоугольный параллелепипед (26,10) Как найти объем прямоугольного параллелепипеда
Как найти объем прямоугольного параллелепипеда Построение сечений параллелепипеда 10 класс
Построение сечений параллелепипеда 10 класс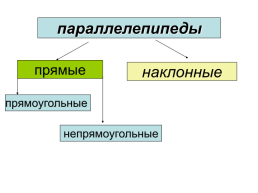 Параллелепипеды. Прямые. Наклонные. Прямоугольные. Непрямоугольные
Параллелепипеды. Прямые. Наклонные. Прямоугольные. Непрямоугольные Тетраэдр - Задачи на построение сечений
Тетраэдр - Задачи на построение сечений