Презентация - Что за чудо эти многогранники?

Что за чудо эти многогранники?
(исследовательская работа) Выполнили работу ученицы 10 «в» класса Брыгина Юлия и Еремеева Татьяна. Руководитель-Макарова Эльвира Викентьевна.

Цель работы:
Изучить правильные многогранники. И ознакомиться с материалами, выходящих за пределы страниц учебника.
Наши задачи:
1. Подробнее ознакомиться с видами многогранников. 2.Развитие пространственного мышления, применение задач. 3.Применение многогранников в действительности. 4.Узнать-нужно ли изучать многогранники.

Гипотеза
Наша гипотеза заключается в том, что наш мир не может существовать без многогранников, и очень важна их роль.

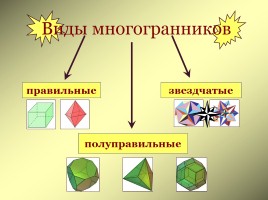
Виды многогранников
правильные
звездчатые
полуправильные

Что же такое правильный многогранник?
Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани – равные друг другу правильные многоугольники; 3) в каждой его вершине сходится одинаковое число ребер; 4) все его двугранные равны. Примером правильного многогранника является куб: он является выпуклым многогранником, все его грани – равные квадраты, в каждой вершине сходятся три ребра, и все двугранные углы куба прямые. Правильный тетраэдр также является правильным многогранником.

Возникает вопрос: сколько существует различных типов правильных многогранников?
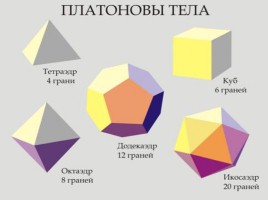
Существуют всего пять видов правильных многогранников

Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Элементы симметрии: Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Тетраэдр

Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер. Элементы симметрии: Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.
Гексаэдр (Куб)

Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер. Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Октаэдр

Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Икосаэдр

Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Элементы симметрии: Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Додекаэдр

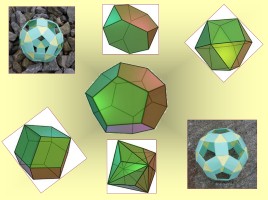
Полуправильные многогранники
Выпуклый многогранник, гранями которого являются правильные многогранники, причем в каждой вершине сходится одинаковое число граней. Представителями таких многогранников является призма, антипризма, бипирамида и т.д.Кросе этих двух бесконечных серий полуправильных многогранников имеются еще только 14 полуправильных многогранников, 13 из которых впервые открыл и описал Архимед. Поэтому эти полуправильные многогранники называются также телами Архимеда.

Что скрывается под звездчатыми многогранниками?
Звездчатые многогранники являются продолжением правильных многогранников. Правильные звездчатые многогранники называются телами Кеплера-Пуансо. Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они в архитектуре. Многие формы звездчатых многогранников показывает сама природа. Снежинки- это звездчатые многогранники.

Снежинки - звездчатые многогранники

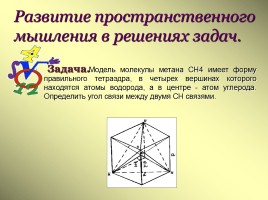
Развитие пространственного мышления в решениях задач.
Модель молекулы метана CH4 имеет форму правильного тетраэдра, в четырех вершинах которого находятся атомы водорода, а в центре - атом углерода. Определить угол связи между двумя СН связями.

Задача.

Решение. Так как правильный тетраэдр имеет шесть равных ребер, то можно подобрать такой куб, чтобы диагонали его граней были ребрами правильного тетраэдра (рис.2). Центр куба является и центром тетраэдра, ведь четыре вершины тетраэдра являются и вершинами куба, а описываемая около них сфера однозначно определяется четырьмя точками, не лежащими в одной плоскости. Искомый угол j между двумя СН связями равен углу АОС. Треугольник АОС-равнобедренный. Отсюда , где а - сторона куба, d- длина диагонали боковой грани или ребро тетраэдра. Итак, , откуда =54,73561О и j= 109,47О

Применение многогранников в действительности
Интересно, что пчелиные ячейки, которые также заполняют пространство без просветов, также являются в идеале геометрическими фигурами. Верхняя часть пчелиной ячейки представляет собой часть ромбододекаэдра.

Многогранность в архитектуре
Великая пирамида в Гизе. Эта грандиозная Египетская пирамида является древнейшим из Семи чудес древности. Кроме того, это единственное из чудес, сохранившееся до наших дней. Во времена своего создания Великая пирамида была самым высоким сооружением в мире. И удерживала она этот рекорд, по всей видимости, почти 4000 л

Вечные строения
Во всем облике японского строения очевидна идея преобразования пространства, подчинения его новой логике - логике "завоевания" природного ландшафта, которому противопоставлена четкая геометрия проникающих архитектурных форм.
Как объясняет создатель Музея Плодов в Яманаши Ицуко Хасегава, одна из немногих преуспевающих японских женщин-архитекторов, "геометрия трех оболочек была проанализирована с помощью объемных компьютерных построений. Каждая форма была образована путем вращения простых геометрических форм до получения сложных объемов

Алмаз-многогранник!
Алмаз (от араб. ألماس‎‎, ’almās, тур. elmas, которое идёт через арабск. из др.-греч. ἀδάμας — «несокрушимый») — минерал, одна из аллотропных форм углерода. Главные отличительные черты алмаза — высочайшая среди минералов твёрдость, наиболее высокая теплопроводность среди всех твёрдых тел, большие показатель преломления и дисперсия. Алмаз является диэлектриком. В 1961 году появились первые публикации фирмы «DuPont» о реализации идей получения алмаза путём прямого фазового перехода из графита. Алмаз уже многие столетия является популярнейшим и дорогим драгоценным камнем. В то время как цена других драгоценных камней определяется модой и постоянно меняется, алмаз остаётся островком стабильности на бурном рынке драгоценностей. Форма огранки бриллианта зависит от формы исходного кристалла алмаза. Чтобы получить бриллиант максимальной стоимости, огранщики стараются свести к минимум потери алмаза при обработке. Алмаз — редкий, но вместе с тем довольно широко распространённый минерал. Промышленные месторождения алмазов известны на всех континентах, кроме Антарктиды. Известно несколько видов месторождений алмазов. Уже несколько тысяч лет назад алмазы в промышленных масштабах добывались из россыпных месторождений. Только к концу XIX века, когда впервые были открыты алмазоносные кимберлитовые трубки, стало ясно, что алмазы не образуются в речных отложениях.

Моделирование многогранников (учащимися )

1.Нужны ли правильные многогранники в жизни? 2.Знаете ли вы о полуправильных, звездчатых многогранниках? 3.Встречались ли тебе многогранники в жизни? 4.Как вы думаете, важно ли их использование в окружающей среде?
Опрос
11
классов

Анализ.
Опрос 11 класса показал, что ученики очень мало знают о назначении многогранников в жизни человека. Учениками усвоен материал геометрии в пределах учебника. На вопрос-знаете ли вы о полуправильных, звездчатых многогранниках?- ответы были отрицательные. Мы думаем, что ученики лишь познали самую малейшую и важную часть темы «многогранники», которая в ходит в учебник геометрии, и не каждый изучает самостоятельно тему «многогранники».

Вывод:
Наша гипотеза подтвердилась. По проведенной исследовательской работе можно сказал, что мы, выполнив поставленные задачи и добившись цели, выяснили: что, действительно, многогранники играет не мало важную роль в окружающей среде и также важно их использование. Непосредственно, тема - изучении многогранников занимает одну из волнующих тем - удобств и нужд людей в действительности. Этой работой мы хотим заинтересовать всех, и дать возможность открыть тайны неизвестного.

Что за чудо эти многогранники?