Презентация - Арифметическая и геометрическая прогрессии

Арифметическая и Геометрическая прогрессии
Проект ученика 9б класса Тесли Дмитрия

Прогрессия
Арифметическая Геометрическая
- числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом  d. Число  d  называется разностью прогрессии. - числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число  q. Число q называется знаменателем прогрессии.

Прогрессия
Арифметическая Геометрическая
Любой член арифметической прогрессии вычисляется по формуле: an=a1+d(n–1)  Сумма  n  первых членов арифметической прогрессии вычисляется так: Sn=0,5(a1+an)n Любой член геометрической прогрессии вычисляется по формуле: bn=b1qn-1  Сумма  n  первых членов геометрической прогрессии вычисляется так: Sn=b1(qn-1)/q-1

Арифметическая прогрессия
Известна интересная история о знаменитом немецком математике К. Гауссе (1777 – 1855), который еще в детстве обнаружил выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за одну минуту, сообразив, что суммы 1+100, 2+99 и т.д. равны, он умножил 101 на 50, т.е. на число таких сумм. Иначе говоря, он заметил закономерность, присущую арифметическим прогрессиям.

Бесконечно убывающая геометрическая прогрессия
- это геометрическая прогрессия, у которой |q|<1. Для нее определяется понятие суммы членов бесконечно убывающей геометрической прогрессии, а именно: это число, к которому неограниченно приближается сумма n первых членов рассматриваемой прогрессии при неограниченном возрастании числа n. Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле: S=b1/1-q.

Арифметическая и геометрическая прогрессии, как оправдание войн
Английский экономист епископ Мальтус использовал геометрическую и арифметическую прогрессии для оправдания войн: средства потребления (пища, одежда) растут по законам арифметической прогрессии, а люди размножаются по законам геометрической прогрессии. Чтоб избавиться от лишнего населения необходимы войны.

Практическое применение геометрической прогрессии
Вероятно, первая ситуация, в которой людям пришлось столкнуться с геометрической прогрессией – подсчет численности стада, проведенный несколько раз, через равные промежутки времени. Если не происходит никаких чрезвычайных ситуаций, количество новорожденных и умерших животных пропорционально числу всех животных. Значит, если за какой-то период времени количество овец у пастуха увеличилось с 10 голов до 20, то за следующий такой же период оно снова вырастит вдвое и станет равным 40.

Экология и промышленность
Прирост древесины в лесном массиве происходит по законам геометрической прогрессии. При этом у каждой породы дерева свой коэффициент годового роста объема. Учет этих изменений позволяет планировать вырубку части лесных массивов и одновременную работу по восстановлению лесов.

Биология
Бактерия за одну секунду делится на три. Сколько бактерий будет в пробирке за пять секунд? Первый член прогрессии – одна бактерия. По формуле найдем, что на вторую секунду мы будем иметь 3 бактерии, на третью - 9, на четвертую - 27, на пятую - 32. Таким образом можно рассчитать количество бактерий в пробирке в любой момент времени.

Экономика
В жизненной практике геометрическая прогрессия появляется в первую очередь в задаче об исчислении сложных процентов. Срочный вклад, положенный в сберегательный банк, ежегодно увеличивается на 5%. Каким станет вклад через 5 лет, если вначале он был равен 1000 рублей? На следующий после вклада год мы будем иметь 1050 рублей, на третий год – 1102,5, на четвертый – 1157,625, на пятый – 1215,50625 рублей.

Физика
Еще один пример геометрической прогрессии – изменение массы радиоактивного вещества со временем. Известно, что за сутки масса радиоактивного вещества, которая изначально была 256 г, уменьшается вдвое. Какова станет масса вещества на пятые сутки? На второй день останется 128 г, на третий – 64 г, на четвертый – 32 г, на пятый – 16 г.

Изобретатель шахмат и король
1 клетка – 1 зерно 2 клетка – 2 зерна 3 клетка – 4 зерна … 64 клетка – 18 446 744 073 709 551 615

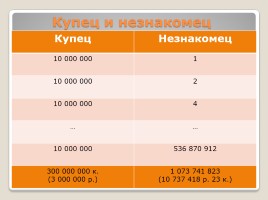
Купец и незнакомец
Купец Незнакомец
10 000 000 1
10 000 000 2
10 000 000 4
… …
10 000 000 536 870 912
300 000 000 к. (3 000 000 р.) 1 073 741 823 (10 737 418 р. 23 к.)

Благодарю за внимание!