Презентация - Геометрические фигуры

Номинация «Геометрические миниатюры» Тема Геометрические фигуры Автор Калиев Алексей (Kaliev alexey) nek2393@bk.ru 8(909)690-98-96 Адрес Московская область, Раменское, Серова, 10

Цели и задачи
Кратко рассказать об основных геометрических фигурах, об их открытиях, формулах, свойствах. Кратко рассказать про историю геометрии и великих ученых-геометрах

Общие понятия
Первоначальные сведения о свойствах геометрических тел люди нашли, наблюдая окружающий мир и в результате практической деятельности. Со временем ученые заметили, что некоторые свойства геометрических тел можно выводить из других свойств путем рассуждения. Геометрия в ранний период своего развития достигла особенно высокого уровня в Египте, а позже в Греции. В это время (период с VII по III век до нашей эры) возникали первые аксиомы, теоремы и доказательства. Многовековая работа ученых-геометров впервые была подытожена Евклидом в его знаменитом труде «Начала».

Выдающиеся геометры

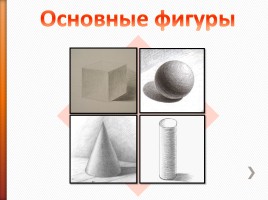
Основные фигуры

Конус
Первым дал определение конуса Пифагор: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом.  Неподвижный катет, вокруг которого поворачивается треугольник, называется осью конуса, а круг, описываемый вращающимся катетом, называется основанием конуса. Евклид рассматривает только прямые конусы, т.е. такие, у которых ось перпендикулярна к основанию, лишь Аполлоний различает прямые и косые конусы, у которых ось образует с основанием угол, отличный от прямого.

Связанные определения
Полная поверхность конуса состоит из основания и боковой поверхности. Конус называется прямым, если прямая соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту. Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением. Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. Центр тяжести любого конуса лежит на четверти высоты считая от основания.

Свойства конуса
Боковая поверхность: S=rl, где r — радиус основания, l — длина образующей. Полная поверхность: S=r(r+l), где r — радиус основания, l — длина образующей. Объем кругового конуса: V=31r2h Телесный угол при вершине прямого кругового конуса: =2(1−cos2), где  — угол раствора конуса (т. е. удвоенный угол между осью конуса и любой прямой на его боковой поверхности).

Сечения конуса
Существует три главных типа конических сечений: эллипс, парабола и гипербола, кроме того существуют вырожденные сечения: точка, прямая и пара прямых. Окружность можно рассматривать как частный случай эллипса.

Пирамида
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был  Демокрит, а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал» , а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.

Элементы пирамиды
апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины; боковые грани — треугольники, сходящиеся в вершине пирамиды; боковые ребра — общие стороны боковых граней; вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания; высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра); диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания; основание — многоугольник, которому не принадлежит вершина пирамиды.

Свойства пирамиды
Объем пирамиды вычисляется по формуле V=1/3Sh, где S — площадь основания и h — высота. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему (правильная четырехугольная пирамида: Sбок = (AB+BC+CD+DA)hs / 2 = P hs / 2) .

Усеченная пирамида
Плоскость, параллельная плоскости основания пирамиды и пересекающая пирамиду, отсекает от неё подобную пирамиду. Другая часть пирамиды представляет собой многогранник, который называют усеченной пирамидой. Объём пирамиды , где S1,S2 — площади оснований, h — высота усечённой пирамиды. Площадь боковой поверхности  равна сумме площадей боковых граней усечённой пирамиды.

Шар
Шар — геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой.

Свойства шара
Площадь шара Объем шара , где r-радиус

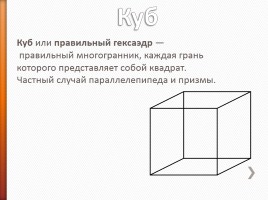
Куб
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.

Свойства куба
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям. В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба. Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра. В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

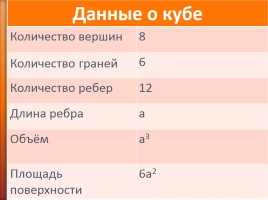
Данные о кубе Данные о кубе
Количество вершин 8
Количество граней 6
Количество ребер 12
Длина ребра a
Объём a3
Площадь поверхности 6a2

Другие фигуры
Цилиндр Параллелепипед Призма Тетраэдр

Список литературы
wikipedia.org uztest.ru geometry.omskhost.ru учебник геометрии 10-11 класс Л.С.Атанасян, В.Ф.Бутузов и др.