Презентация - Построение графика квадратичной функции

1
Построение графика квадратичной функции
Учитель математики ГБОУ СОШ N 234 Адмиралтейского р-на Санкт-Петербурга Петрова В.Д.

2
Цели и задачи урока: Освоить алгоритм построения графика квадратичной функции. Научиться преодолевать трудности, работать в коллективе. Научиться работать с источниками информации. Строить самостоятельно графики квадратичной функции.

3
Проверка домашнего задания. N 621(нч), 622(нч),624 (1),626.
№ 621. Координаты вершины параболы: 1) (-2;7) , 3) (-1;6). № 622. Координаты точек пересечения параболы с осями координат: 1) D = 9 – 20 = -11 , D<0 , с осью ОХ график параболы не пересекается. с = 5 - с осью OY график параболы пересекается в точке (0;5). 3) ,- с осью OX, - с осью OY.

4
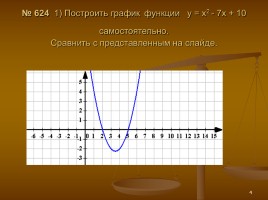
№ 624 1) Построить график функции y = x2 - 7x + 10 самостоятельно. Сравнить с представленным на слайде.

5
1) y>o при x<2 и x>5 или y>0 на промежутке (- беск. ;2), (5;+беск. ) y<0 при 2

6
Задача № 326 (в парах)
х – первое число, (15 – х) – второе число, произведение х(15 – х) будет наибольшим в той точке , где функция y = x(15 – x), y = – x2 +15x имеет максимум X0 = - 15:(- 2) = 7,5 Ответ: 7,5 и 7,5.

7
Схема построения графика квадратичной функции.
Определить по формуле а, b, с и направление ветвей параболы. Построить вершину параболы (хо; yo): xo= ; yo=y(xo). Провести через вершину параболы прямую, параллельную оси ординат, - ось симметрии параболы. Найти нули функции, если они есть, x1,2= и построить на оси абсцисс точки (х1; 0) и (х2;0). Построить еще две точки параболы симметричные относительно ее оси. Например, точки (0; c) и (2хо; c), если хо0. Полезно найти еще несколько точек для более точного построения графика. Через полученные точки провести параболу.

8
Задание.
Построить график функции y = -2x2+3x+2. Выяснить ее свойства.

9
Литература
Алимов Алгебра 8