Презентация - Теория вероятностей в заданиях ЕГЭ

1. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение: Обозначим через А событие «команда России во второй группе». Тогда количество благоприятных событий m = 4 (четыре карточки с номером 2), а общее число равновозможных событий n = 16 (16 карточек).
Ответ: 0,25.
02.10.2015
Антонова Г.В.

2. В чемпионате мира участвуют 15 команд. С помощью жребия их нужно разделить на пять групп по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Италии окажется в третьей группе?
Решение: Обозначим через А событие «команда Италии в третьей группе». Тогда количество благоприятных событий m = 3 (три карточки с номером 3), а общее число равновозможных событий n = 15 (15 карточек).
 
Ответ: 0,2.
02.10.2015
Антонова Г.В.

3. Конкурс исполнителей проводится в 4 дня. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
 
Ответ: 0,25.
02.10.2015
Антонова Г.В.

4. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов – первые три дня по 17 докладов, остальные распределены поровну между четвёртым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?
 
Ответ: 0,16.
02.10.2015
Антонова Г.В.

5. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление представителя России состоится в третий день конкурса?
 
 
Ответ: 0,225.
02.10.2015
Антонова Г.В.

6. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 5 прыгунов из Испании и 3 прыгуна из Бразилии. Порядок выступлений определяется жребием. Найдите вероятность того, что сорок вторым будет выступать прыгун из Испании.
 
Ответ: 0,1.
02.10.2015
Антонова Г.В.

7. В классе 21 шестиклассник, среди них два друга – Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в одной и той же группе.
Решение: В каждой группе 7 человек. Будем считать, что Митя уже занял место в одной группе. Обозначим через А событие «Петя оказался в той же группе». Для Пети останется n = 20 свободных мест, из них m = 6 мест.
Ответ: 0,3.
02.10.2015
Антонова Г.В.

8. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.
Решение: Общее число случаев (число участников, исключая самого Руслана Орлова) n = 26 – 1 = 25.
Число благоприятных случаев (число участников из России, исключая самого Руслана Орлова) m = 10 – 1 = 9.
 
Ответ: 0,36.
02.10.2015
Антонова Г.В.

9. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Найдите вероятность того, что мишень будет поражена (одним из выстрелов).
 
 
02.10.2015
Антонова Г.В.

 
Ответ: 0,84.
02.10.2015
Антонова Г.В.

10. Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 25% этих стёкол, вторая – 75%. Первая фабрика выпускает 4% бракованных стёкол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
 
 
Ответ: 0,025.
02.10.2015
Антонова Г.В.

11. Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40% предохранителей, второй – 60%. Первый завод выпускает 4% предохранителей, а второй – 3%. Найдите вероятность того, что случайно выбранный в магазине предохранитель окажется бракованным.
 
 
Ответ: 0,034.
02.10.2015
Антонова Г.В.

12. На соревнования по метанию ядра приехали 5 спортсменов из Сербии, 7 из Хорватии и 3 из Норвегии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Норвегии
Решение: Общее число случаев (число всех спортсменов) n = 15. Число благоприятных случаев (число спортсменов из Норвегии) m = 3.
 
Ответ: 0,2.
02.10.2015
Антонова Г.В.

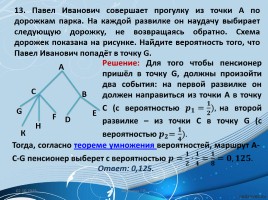
13. Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.
 
 
Ответ: 0,125.
02.10.2015
Антонова Г.В.

14. Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение: Обозначим через A событие «начинает игру Петя». Тогда количество благоприятствующих исходов m = 1, а общее число равновозможных исходов n (начинает игру Петя, начинает игру Вася, начинает игру Коля, начинает игру Лёша).
Ответ: 0,125.
02.10.2015
Антонова Г.В.

15. Катя дважды бросает игральный кубик. В сумме у неё выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.
Общее число случаев n = 5 ((1,5); (5,1); (2,4); (4,2); (3,3)). Число благоприятных случаев (комбинации (1,5); (5,1)) m = 2.
Ответ: 0,4.
02.10.2015
Антонова Г.В.
Решение:

16. Люда дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при первом броске выпало 5 очков.
Решение: Общее число случаев n = 4 ((3,6); (4,5); (5,4); (6,3)). Число благоприятных случаев m = 1 (комбинация (5,4)).
 
Ответ: 0,25.
17. Таня и Нина играют в кости. Они бросают кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 6 очков. Найдите вероятность того, что Таня выиграла.
Решение: Общее число случаев n = 5 ((1,5); (2,4); (3,3); (4,2); (5,1)). Число благоприятных случаев m = 2 (комбинации (1,5); (2,4) или (4,2); (5,1)).
 
Ответ: 0,4.
02.10.2015
Антонова Г.В.

18. Найдите вероятность того, что при бросании двух кубиков на каждом выпадет менее 4 очков.
 
Ответ: 0,25.
19. При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало меньше 3 очков.
Решение: Общее число случаев n = 5 (комбинации (1,5); (5,1); (2,4); (4,2); (3,3)). Число благоприятных случаев (комбинации (1,5); (2,4)) m = 2.
 
Ответ: 0,4.
02.10.2015
Антонова Г.В.

20. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Меркурий» по очереди играет с командами «Марс», «Юпитер» и «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда «Меркурий».
 
Ответ: 0,125.
02.10.2015
Антонова Г.В.

 
 
Ответ: 0,125.
02.10.2015
Антонова Г.В.
2 способ решения:

21. Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Хуторянка» по очереди играет с командами «Радуга», «Дружба», «Заря» и «Воля». Найдите вероятность того, что команда «Хуторянка» будет первой владеть мячом только в первых двух играх.
 
 
Ответ: 0,0625.
02.10.2015
Антонова Г.В.

22. Перед началом матча по водному поло судья устанавливает мяч в центр бассейна, и от каждой команды к мячу плывёт игрок, чтобы первым завладеть мячом. Вероятность выиграть мяч у игроков равны. Команда «Русалочка» по очереди играет с командами «Наяда», «Ундина» и «Ариэль». Найдите вероятность того, что во втором матче команда «Русалочка» выиграет мяч в начале игры, а в двух других проиграет
 
 
Ответ: 0,125.
02.10.2015
Антонова Г.В.

23. В некоторой местности утро в июле может быть либо ясным, либо пасмурным. Наблюдения показали: 1) Если июльское утро ясное, то вероятность дождя в этот день 0,1. 2) Если июльское утро пасмурное, то вероятность дождя в течение дня равна 0,5. 3) Вероятность того, что утро в июле будет пасмурным, равна 0,2. Найдите вероятность того, что в случайно взятый июльский день дождя не будет.
02.10.2015
Антонова Г.В.

 
 
 
Ответ: 0,82.
02.10.2015
Антонова Г.В.

24. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение: Первый способ. Обозначим через А событие «кофе закончится в первом автомате», через В событие «кофе закончится во втором автомате». Событие С «кофе закончится хотя бы в одном автомате» является их суммой С = А + В.
 
 
02.10.2015
Антонова Г.В.

 
 
Ответ: 0,52.
02.10.2015
Антонова Г.В.
Решение: Второй способ решения задачи 16.

25. В сборнике билетов по математике всего 20 билетов, в 7 из них встречается вопрос о производной. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не встретится вопрос о производной.
Решение: Общее число случаев (всего билетов) n = 20. Число благоприятных случаев (количество билетов, в которых не встречается вопрос о производной) m = 20 – 7 = 13.
 
Ответ: 0,65.
02.10.2015
Антонова Г.В.

26. В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика.
 
 
Ответ: 0,1.
02.10.2015
Антонова Г.В.

27. Валя выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 51.
 
 
Ответ: 0,1.
02.10.2015
Антонова Г.В.

Формула классической вероятности
Вероятность – есть число, характеризующее возможность наступления события.
 
Сумма вероятностей всех элементарных событий случайного эксперимента равна 1.
02.10.2015
Антонова Г.В.

Несовместные события. Формула сложения вероятностей
Определение. События называют несовместными, если они не могут происходить одновременно в одном и том же испытанию
Например, выигрыш, ничейный исход и проигрыш одного игрока в одной партии в шахматы – три несовместных события.
Теорема. Вероятность суммы двух несовместных событий A и B (появление хотя бы одного события) равна сумме вероятностей этих событий: P (A+B)=P(A) +P(B).
Теорема обобщается на любое число попарно несовместных событий
 
02.10.2015
Антонова Г.В.

Совместные события. Формула сложения вероятностей (формула для вероятности суммы двух событий в общем случае (не обязательно несовместных))
Определение. События называют совместными, если они могут происходить одновременно. Например, при бросании двух монет выпадение решки на одной не исключает появление решки на другой монете.
Теорема. Вероятность суммы двух совместных событий A и B (появление хотя бы одного события) равна сумме их вероятностей без вероятности их совместного появления, то есть P (A+B)=P(A) +P(B) – P(AB).
02.10.2015
Антонова Г.В.

Независимые события. Формула умножения вероятностей
Определение. Два случайных события называют независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события называют зависимыми.
Теорема. Вероятность произведения (совместного появления) двух независимых событий равна произведению вероятностей этих событий: P(AB) = P(A) · P(B).
02.10.2015
Антонова Г.В.

Использованная литература: ЕГЭ-2014: Математика: самое полное издание типовых вариантов заданий/ авт.-сост. И.В.Ященко, И.Р. Высоцкий; под ред. А.Л.Семёнова, И.В.Ященко.- Москва: АСТ: Астрель, 2014. А.Г.Корянов , Н.В.Надежкина. Задача В10. ЕГЭ. Математика, 2014. Элементы теории вероятностей (интернет-ресурс http://alexlarin.net/ege/2014/b102014.html‎) ЕГЭ: 3000 задач с ответами по математике. Все задания группы В/А.Л.Семёнов, И.В.Ященко и др.; под ред. А.Л.Семёнова, И.В.Ященко. – М.: Издательство «Экзамен», 2014. Источник шаблона презентации : http://pedsovet.su/load/321-1-0-32889
02.10.2015
Антонова Г.В.