Презентация - Алгоритмы Прима и Крускала построения остовного связного дерева минимального веса

Алгоритмы Прима и Крускала построения остовного связного дерева минимального веса
Гуляева Татьяна Викторовна
учитель информатики и математики МБОУ СОШ №9 с УИОП г.Павлово
2014 год

Содержание
Повторение основных понятий теории графов Понятие остовного связного дерева Понятие цикломатического числа Алгоритм Прима Алгоритм Крускаля Вопросы и задания

Основные понятия теории графов
По горизонтали:
г р а ф
9. Наглядное сред-ство представления состава и структуры системы.  
р е б р о
2. Ненаправленная линия (без стрелки), соединяющая вершины графа.  
п у т ь
ц и к л
п у с т о й
д у г а
д е р е в о
в е р ш и н а
в з в е ш е н н ы й
4. Последователь-ность рёбер и/или дуг, такая, что конец одной дуги (ребра) является началом другой дуги (реб-ра).  
5. Путь, в котором совпадают начальная и конечная верши-ны.  
6. Направленная ли-ния (со стрелкой), соединяющая верши-ны графа.  
7. Граф без ребер.  
10. Граф, в котором нет циклов.  
11. Элемент (точка) графа, обозначаю-щий объект любой природы, входящий в множество объек-тов, описываемое графом.  
12. Граф, ребрам (или дугам) или вершинам которого поставлены в соот-ветствие числовые величины.  
Перейдем к вопросам по вертикали  

Основные понятия теории графов
По вертикали:
г р а ф
р е б р о
п у т ь
ц и к л
п у с т о й
д у г а
д е р е в о
в е р ш и н а
в з в е ш е н н ы й
1. Последовательность чередующихся вершин и ребер графа при перемещении.  
м а ш р т
с м ж ы
8. Вершины, прилега-ющие к одному и тому же ребру.  
3. Граф, в котором вершины соединены дугами.  
о н ы
4. Граф, в котором каждые две вершины смежные.  
Перейдем к изучению новых понятий

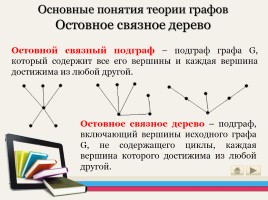
Основные понятия теории графов Остовное связное дерево
Остовной связный подграф – подграф графа G, который содержит все его вершины и каждая вершина достижима из любой другой.
Остовное связное дерево – подграф, включающий вершины исходного графа G, не содержащего циклы, каждая вершина которого достижима из любой другой.

Цикломатическое число γ показывает, сколько ребер нужно удалить из графа, чтобы в нем не осталось циклов
Основные понятия теории графов Цикломатическое число
γ = m – n + 1, m - количество ребер n - количество вершин

Задача 1
В некотором районе было решено провести газопровод между пятью деревнями. От Кошкино до Мышкино идти 10 км, от Мышкино до Ступино – 3 км, от Кошкино до Малаховки – 6 км, от Малаховки до Черняевки – 12 км, от Кошкино до Ступино – 11 км, от Мышкино до Чернеевки – 5 км, от Кошкино до Чернеевки – 7 км. Как необходимо провести трубу, чтобы она соединяла все пять деревень, и затраты при этом были минимальными?

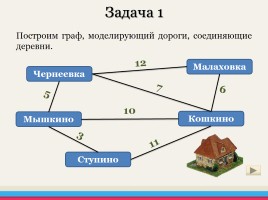
Задача 1
Построим граф, моделирующий дороги, соединяющие деревни.

Задача 1
Задача сводится к построению остовного связного дерева минимального веса.
Рассчитаем цикломатическое число.
m (количество ребер) равно 7 n (количество вершин) рано 5 γ = 7 – 5 + 1 = 3
Т.е. три деревни напрямую соединены газовой трубой не будут.
(переходы по щелчку)

Алгоритм Прима
Пусть дан взвешенный неориентированный граф. Для построения минимального остовного дерева необходимо:
1. Представить граф в виде матрицы смежности
2. Найти в матрице наименьший элемент, соответству-ющий ребру, соединяющему i-ю и j-ю вершины графа
3. Вычеркнуть элементы i-й и j-й строки матрицы
4. Пометить i-й и j-й столбцы матрицы
5. В помеченных столбцах i и j найти наименьший элемент, отличный от уже найденного
6. Повторять пункты 3-5 до тех пор, пока не будут задействованы все вершины графа
(переходы по щелчку)

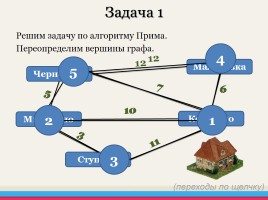
Задача 1
Решим задачу по алгоритму Прима. Переопределим вершины графа.
(переходы по щелчку)

Задача 1
Представим граф в виде матрицы смежности.
Найдем минимальный элемент.
Он равен 3
1 2 3 4 5
1 0 10 11 6 7
2 10 0 3 0 5
3 11 3 0 0 0
4 6 0 0 0 12
5 7 5 0 12 0
3
3
(переходы по щелчку)

1 2 3 4 5
1 0 10 11 6 7
2 3
3
4 6 0 0 0 12
5 7 5 0 12 0
1 2 3 4 5
1 0 10 11 6 7
2 10 0 3 0 5
3 11 3 0 0 0
4 6 0 0 0 12
5 7 5 0 12 0
1 2 3 4 5
1 0 10 11 6 7
2 3
3
4 6 0 0 0 12
5 7 5 0 12 0
Задача 1
Вычеркнем 2-ю и 3-ю строки таблицы. А столбцы 2 и 3 выделим.
Найдем минимальный элемент в выделенных столбцах.
Он равен 5
5
(переходы по щелчку)

1 2 3 4 5
1 0 10 11 6 7
2 3
3
4 6 0 0 0 12
5 7 5 0 12 0
1 2 3 4 5
1 0 10 11 6 7
2 3
3
4 6 0 0 0 12
5 5
Задача 1
Вычеркнем 5-ю строку таблицы. А столбец 5 выделим.
Найдем минимальный элемент в выделенных столбцах.
Он равен 7
5
7
(переходы по щелчку)

1 2 3 4 5
1 0 10 11 6 7
2 3
3
4 6 0 0 0 12
5 5
1 2 3 4 5
1 7
2 3
3
4 6 0 0 0 12
5 5
Задача 1
Вычеркнем 1-ю строку таблицы. А столбец 1 выделим.
Найдем минимальный элемент в выделенных столбцах.
Он равен 6
5
(переходы по щелчку)

1 2 3 4 5
1 7
2 3
3
4 6 0 0 0 12
5 5
1 2 3 4 5
1 7
2 3
3
4 6
5 5
Задача 1
Вычеркнем 4-ю строку таблицы. А столбец 4 выделим.
(переходы по щелчку)

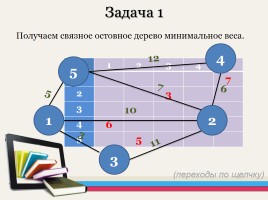
Задача 1
Получаем связное остовное дерево минимальное веса.
1 2 3 4 5
1 7
2 3
3
4 6
5 5
12
7
10
11
3
6
5
5
1
2
3
4
(переходы по щелчку)

Задача 1
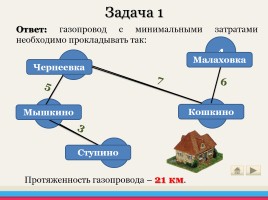
Ответ: газопровод с минимальными затратами необходимо прокладывать так:
Протяженность газопровода – 21 км.

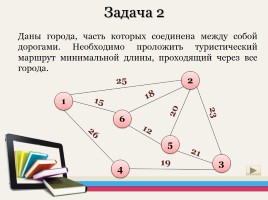
Задача 2
Даны города, часть которых соединена между собой дорогами. Необходимо проложить туристический маршрут минимальной длины, проходящий через все города.

Задача 2
Задача сводится к построению остовного связного дерева минимального веса.
Рассчитаем цикломатическое число.
m (количество ребер) равно 9 n (количество вершин) рано 6 γ = 9 – 6 + 1 = 4
Т.е. четыре дороги, соединяющие города, не будут включены в туристический маршрут.
(переходы по щелчку)

Алгоритм Крускала
Удалить все ребра и получить остовной подграф с изолированными вершинами. Отсортировать ребра по возрастанию. Ребра последовательно, по возрастанию их весов, включаются в остовное дерево. Возможны случаи: а) обе вершины включаемого ребра принадлежат одноэлементным подмножествам, тогда они объединяются в новое, связное подмножество; б) одна из вершин принадлежит связному под-множеству, другая нет, тогда включаем вторую в подмножество, которому принадлежит первая; в) обе вершины принадлежат разным связным подмножествам, тогда объединяем подмножества; г) обе вершины принадлежат одному связному подмножеству, тогда исключаем данное ребро. Алгоритм завершается, когда все вершины будут объединены в одно множество.

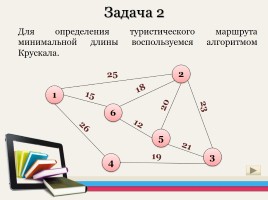
Задача 2
Для определения туристического маршрута минимальной длины воспользуемся алгоритмом Крускала.

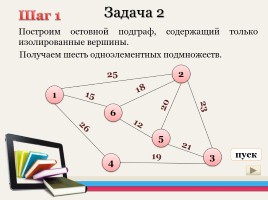
Задача 2
Построим остовной подграф, содержащий только изолированные вершины.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Шаг 1
Получаем шесть одноэлементных подмножеств.
пуск

Задача 2
Найдем ребро минимального веса и добавим его в остовной подграф.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Шаг 2
Образуется связное подмножество вершин {V5, V6}.
пуск

Задача 2
Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Шаг 3
Добавляем в подмножество вершин еще одну {V5,V6,V1}.
пуск

Задача 2
Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Шаг 4
Добавляем в подмножество вершин еще одну {V5,V6,V1,V2}.
пуск

Задача 2
Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Шаг 5
Образуется два подмножества {V5,V6,V1,V2} и {V3,V4} .
пуск

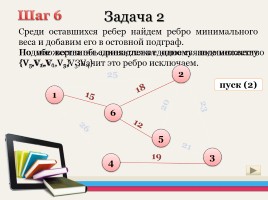
Но обе вершины принадлежат одному подмножеству {V5,V6,V1,V2}. Значит это ребро исключаем.
Задача 2
Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Шаг 6
Подмножества объединяются в единое связное множество {V1,V2,V6,V5,V3,V4} .
пуск (2)

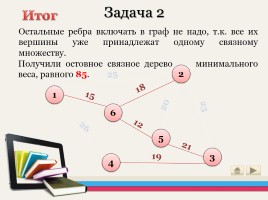
Задача 2
Остальные ребра включать в граф не надо, т.к. все их вершины уже принадлежат одному связному множеству.
1
6
5
2
3
4
25
18
15
12
20
23
21
19
26
Итог
Получили остовное связное дерево минимального веса, равного 85.

Вопросы
Построенный граф (в задачах 1 и 2) является
Почему?
В граф включены все вершины
Все вершины в графе можно соединить маршрутами
В графе отсутствуют циклы
В граф последовательно включались ребра, отсортированные по возрастанию весов
остовным
связным
деревом
с минимальным весом

Задача 3
На строительном участке необходимо создать телефонную сеть, соединяющую все бытовки. Для того, чтобы телефонные линии не мешали строительству, их решили проводить вдоль дорог. Схема участка изображена на рисунке.
Каким образом провести телефонные линии, чтобы их общая длина была минимальной?
Ответ
Общая длина телефонной линии равна 930 метров

Источники
Кроссворд создан на сайте и расположен по адресу http://puzzlecup.com/?guess=3C2D4A01E0522AAU Информатика и ИКТ. Профильный уровень: учебник для 11 класса / Н.Д.Угринович. – М.: Бином. Лаборатория знаний, 2010. Алгоритм Прима-Крускала (видео) http://www.youtube.com/watch?v=vm_9-vnV7PE Занимательные задачи по теории графов: Учеб.-метод. пособие/ О.И.Мельников. – Изд-е 2-е, стереотип. – Мн.: «ТетраСистемс», 2001

Источники изображений
Изображение деревенского дома http://www.diorama.com.ua/images/product_images/popup_images/2074_1.jpg Изображение связных деревьев http://xreferat.ru/image/54/1306491707_19.png
выход