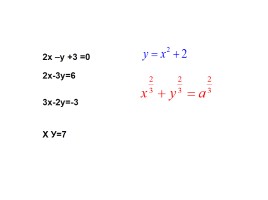Слайды и текст этой онлайн презентации
Слайд 1
1. Является ли пара чисел (–1; 3) решением системы уравнений:
2х+у=1
х-у= -4
Слайд 2
Что значит графически решить систему уравнений?
Слайд 3
2х –у +3 =0
2х-3у=6
3х-2у=-3
Х У=7
Слайд 4
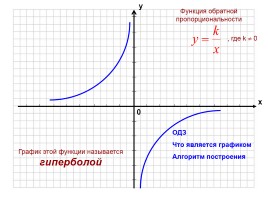
График этой функции называется гиперболой
ОДЗ
Что является графиком
Алгоритм построения
Слайд 6
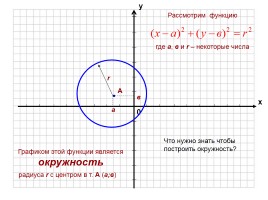
Что нужно знать чтобы построить окружность?
Слайд 7
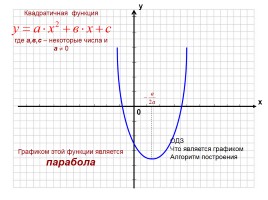
Графиком этой функции является парабола
ОДЗ
Что является графиком
Алгоритм построения
Слайд 8
у = -х2 + 2х + 5;
у = х2 + 2х + 5;
Слайд 9
Алгоритм графического способа решения системы двух уравнений
1
2
3
4
х2 + у2 = 25
у = -х2 + 2х + 5
Слайд 10
Помните о двух вещах!
Если точек пересечения графиков нет, то система решений не имеет;
Координаты точек пересечения определяются приблизительно, поэтому и решения могут получиться приблизительными;
Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы!
Чтобы решить систему двух уравнений с двумя неизвестными, нужно:
Построить в одной системе координат графики уравнений, входящих в систему;
Определить координаты всех точек пересечений графиков (если они есть);
Координаты этих точек и будут решениями системы.
Дальше
Слайд 11
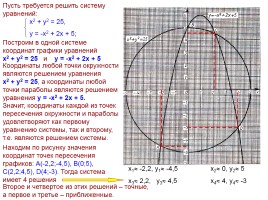
Построим в одной системе координат графики уравнений
х2 + у2 = 25 и у = -х2 + 2х + 5
Координаты любой точки окружности являются решением уравнения х2 + у2 = 25, а координаты любой точки параболы являются решением уравнения у = -х2 + 2х + 5.
Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением системы.
Находим по рисунку значения координат точек пересечения графиков: А(-2,2;-4,5), В(0;5),
С(2,2;4,5), D(4;-3). Тогда система имеет 4 решения
х1 -2,2, у1 -4,5 х2 0, у2 5
х3 2,2, у3 4,5 х4 4, у4 -3
Второе и четвертое из этих решений – точные,
а первое и третье – приближенные.
 Открытый урок по математике. Графический метод решения систем уравнений с двумя переменными
Открытый урок по математике. Графический метод решения систем уравнений с двумя переменными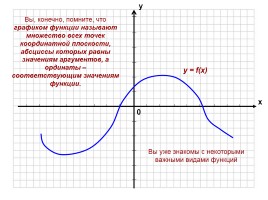 Графический способ решения систем уравнений
Графический способ решения систем уравнений Решение систем уравнений второй степени урок закрепления знаний. Борисова в.С. Учитель математики мбоу сош №11
Решение систем уравнений второй степени урок закрепления знаний. Борисова в.С. Учитель математики мбоу сош №11 Что значит жить по правилам
Что значит жить по правилам Графическое. Решение. Алгебра 8 класс. Уравнений. Квадратных
Графическое. Решение. Алгебра 8 класс. Уравнений. Квадратных Что значит жить по правилам
Что значит жить по правилам Что такое моделирование? Графические информационные модели
Что такое моделирование? Графические информационные модели