Слайды и текст этой онлайн презентации
Слайд 1
Математика
6 класс
Слайд 2
=
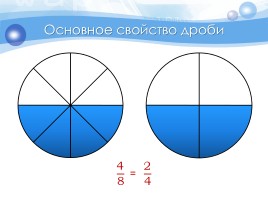
Основное свойство дроби
Две равные дроби являются различными записями одного и того же числа.
Слайд 3
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Слайд 4
=
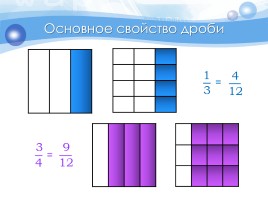
Основное свойство дроби
Слайд 5
=
=
Основное свойство дроби
Слайд 6
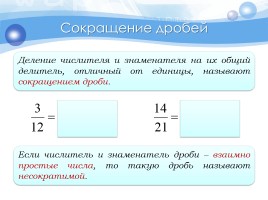
Сокращение дробей
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
Если числитель и знаменатель дроби – взаимно простые числа, то такую дробь называют несократимой.
Слайд 7
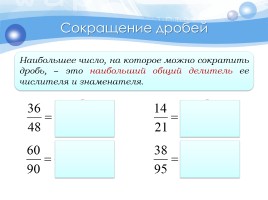
Сокращение дробей
Наибольшее число, на которое можно сократить дробь, − это наибольший общий делитель ее числителя и знаменателя.
Слайд 8
Сокращение дробей разложением на множители
Слайд 9
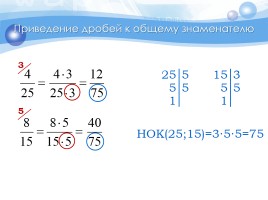
Приведение дробей к общему знаменателю
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.
Любые две дроби можно привести к одному и тому же знаменателю, или иначе к общему знаменателю.
Слайд 10
Приведение дробей к общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю, надо:
найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Слайд 11
Приведение дробей к общему знаменателю
3
5
НОК(25;15)=3∙5∙5=75
Слайд 12
Приведение дробей к общему знаменателю
5
7
НОК(49;35)=7∙7∙5=245
Слайд 13
Сложение и вычитание дробей с разными знаменателями
Слайд 14
Сравнение, сложение и вычитание дробей с разными знаменателями
Чтобы сравнить (сложить или вычесть) дроби с разными знаменателями, надо:
1) привести данные дроби к наименьшему общему знаменателю;
2) сравнить (сложить или вычесть) полученные дроби.
Слайд 15
Сравнение дробей с разными знаменателями
3
5
⇒
Слайд 16
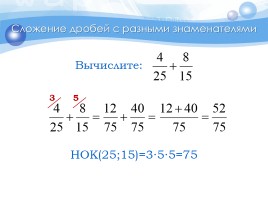
Сложение дробей с разными знаменателями
3
5
НОК(25;15)=3∙5∙5=75
Слайд 17
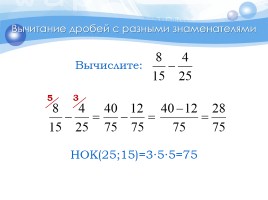
Вычитание дробей с разными знаменателями
5
3
НОК(25;15)=3∙5∙5=75
Слайд 18
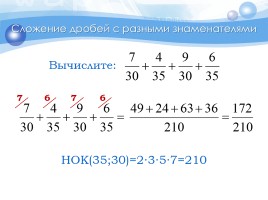
Сложение дробей с разными знаменателями
6
7
НОК(35;30)=2∙3∙5∙7=210
7
6
Слайд 19
Сложение и вычитание дробей с разными знаменателями
4
НОК(60;15)=2∙2∙3∙5=60
1
Слайд 20
Сложение и вычитание смешанных чисел
1
2
Слайд 21
Сложение и вычитание смешанных чисел
2
1
Слайд 22
Сложение и вычитание смешанных чисел
Слайд 23
Сложение и вычитание смешанных чисел
1
2
Слайд 24
Сложение и вычитание смешанных чисел
2
1
 Сложение чисел с разными знаками (урок ФГОС в 6 классе по математике)
Сложение чисел с разными знаками (урок ФГОС в 6 классе по математике) Математика 5 класс «Десятичные дроби»
Математика 5 класс «Десятичные дроби» Урок математики в 5 классе «Доли - Обыкновенные дроби»
Урок математики в 5 классе «Доли - Обыкновенные дроби» Урок математики в 5 классе «Обыкновенные дроби»
Урок математики в 5 классе «Обыкновенные дроби» Урок математики 4 класс «Сложение дробей с одинаковыми знаменателями»
Урок математики 4 класс «Сложение дробей с одинаковыми знаменателями» Математика в жизни моей семьи дроби. 6 Класс
Математика в жизни моей семьи дроби. 6 Класс Математика 2 класс «Деление»
Математика 2 класс «Деление»