Презентация - Математика в музыке

Математика в музыке

Вступление
А знаете ли вы, Что музыка приятная на слух Законам математики подвластна Лечит, оздоравливает дух. Как математика в музыку вошла, Какими законами правит там она, Кто первым математику и музыку соединил, Кто на практике теорию музыки подтвердил. Узнать вы можете сейчас , Читая слайды презентации у нас.

Содержание
1. Школа мудрости 2. Математический подход 3. Основы звука 4. Уравнение колебания струны 5. Музыкальные интерпретации 6. Обозначение звуков 7. Биологические основы звука 8. О соотношении математического обоснова-ния и психологического воздействия музыки 9. Высказывания знаменитостей 10. Вывод.

Исследованию музыки посвящали свои работы многие величайшие математики: Рене Декарт(1), Готфрид Лейбниц(2), Жан д'Аламбер(3), Леонард Эйлер(4), Даниил Бернулли(5). Первым, кто попытался выразить красоту музыки с помощью чисел, был Пифагор - тот самый, чьим именем названа знаменитая теорема.
Величайшие математики и музыка
1.
2.
3.
4.
5.

Школа мудрости 
Началось все еще в древности, когда не было разделения на гуманитарные и естественные науки. Наука рассматривалась как одно целое. Древнегреческий ученый Пифагор и его последователи занимались изучением арифметики, геометрии, астрономии, музыки. Каждая дисциплина исследовала число в разных аспектах: математика- число само по себе, геометрия- число в пространстве, музыка- число во времени, а астрономия- число в пространстве и времени. Именно числа, по мнению Пифагора, управляют гармониями в музыке. Он утвердил музыку как точную науку.

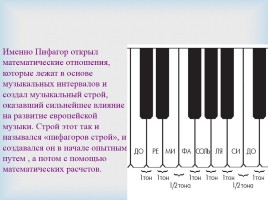
Именно Пифагор открыл математические отношения, которые лежат в основе музыкальных интервалов и создал музыкальный строй, оказавший сильнейшее влияние на развитие европейской музыки. Строй этот так и назывался «пифагоров строй», и создавался он в начале опытным путем , а потом с помощью математических расчетов.

Пифагор создал свою школу мудрости, положив в ее основу два искусства - музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга.

Пространственное представление, столь необходимое ученику в овладении письмом, столь же важно и в математике. Из-за его отсутствия дети не могут подписать в столбик цифры при арифметических действиях, правильно понять условие задач, особенно на время, скорость и расстояние, ошибаются в устном арифметическом счете.

При дальнейшем обучении у таких детей обнаруживается неспособность следить за правильной последовательностью выполнения арифметических действий, например, сложение и вычитание производить только после выполнения умножения и деления. А когда наступает время знакомства с геометрией, попытки одолеть ее полностью терпят крах, потому что овладение этим предметом без пространственного представления невозможно.

Математический подход
Кроме того, школьники часто делают математические ошибки из-за того, что не владеют математическими символами: они не могут следить за математическими знаками «+» и «-», путают знак «<» со знаком «>». Музыка помогает преодолеть эти затруднения на самом начальном этапе, так как знание музыкальной символики приучает к владению обозначениями любыми, в том числе и математическими.

Основы звука
Звук - есть воспринимаемые человеческим слухом колебания воздуха.

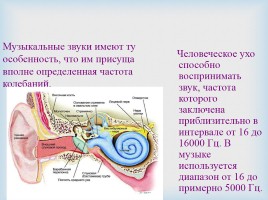
Музыкальные звуки имеют ту особенность, что им присуща вполне определенная частота колебаний.
Человеческое ухо способно воспринимать звук, частота которого заключена приблизительно в интервале от 16 до 16000 Гц. В музыке используется диапазон от 16 до примерно 5000 Гц.

Уравнение колебания струны.
Колебания струны изучали ещё пифагорейцы. Они использовали для этого несложный прибор под названием монохорд, представляющий из себя единственную струну, закрепленную в двух точках над резонатором. Изучая высоту звука с помощью монохорда, именно Пифагор обнаружил удивительные вещи. Выяснилось, что принятые слуху созвучия- консонансы, получаются лишь в том случае, когда длины струн, издающих эти звуки, соотносятся как целые числа первой четверки, т.е. 1:2, 2:3, 3:4. Это открытие потрясло Пифагора: оказалось, что звук и созвучие могут быть описаны простыми числами.

В геометрии есть такое понятие – золотое сечение. Интересно отметить, что это явление обнаруживается и в музыке. Композиция многих музыкальных произведений содержит высшую точку - кульминацию. И размещается эта кульминация чаще не в середине произведения, она смещена, и находится как раз в точке золотого сечения.
Золотое сечение

Золотое сечение или «божественное деление» - это такое деление целого на две неравные части, при котором большая часть AC так относится к целому AB, как меньшая BC к большей AC.

Значительно позже, в XVIII веке, после работ Ньютона и Лейбница в области физики и дифференциального исчисления, было выведено уравнение колебания струны - так называемое волновое уравнение, породившее новую область в науке- математическую физику.

Каждая функция n представляет собой гармоническое колебание с частотой и фазой , где l – длина струны.Амплитуда же колебаний для разных точек разная. На концах струна неподвижна. Все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами. Неподвижные точки называются узлами стоячей волны. Посредине между узлами расположены точки, в которых отклонения достигают максимума. Эти точки назывются пучностями стоячей волны.

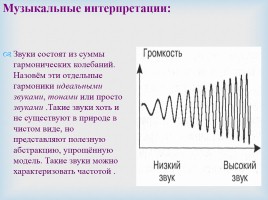
Музыкальные интерпретации:
Звуки состоят из суммы гармонических колебаний. Назовём эти отдельные гармоники идеальными звуками, тонами или просто звуками .Такие звуки хоть и не существуют в природе в чистом виде, но представляют полезную абстракцию, упрощённую модель. Такие звуки можно характеризовать частотой .

Реальный звук струны состоит из звука основной частоты , а также обертонов (верхних тонов, гармоник) - . Такой сложный звук, состоящий из основного тона и обертонов, называется в немецком языке Klang. Основной тон иногда для удобства называют первым обертоном. Соотношение частот обертонов к основному тону даёт нам ряд натуральных чисел: 1, 2, 3, ...

Звуки, не имеющие основной частоты вовсе (и не описывающиеся волновым уравнением) назовем шумами и не будем рассматривать вовсе.

Именно сочетание обертонов даёт музыкальную окраску звуку - его тембр. Если слегка прикоснуться к струне в некоторой точке, то все гармоники, имеющие в этой точке пучность, будут погашены и не будут слышны. Так можно явно услышать вклад обертонов в общий тембр звука.  

В музыке нам интересен не конкретный звук в отдельности, а соотношения звуков друг к другу. Под интервалом понимается расстояние между двумя звуками. При этом нижний звук (с меньшей частотой) называется основанием интервала , а верхний звук (с большей частотой) – его вершиной.

Расстояние можно измерять по-разному, поэтому существуют разные понятия интервала, которые иногда одинаково обозначаются в музыке, что привносит путаницу. На физическом уровне у нас есть только частоты. Акустическим интервальным коэффициентом между двумя звуками назовем частное от деления частоты вершины на частоту основания.

Примой называется акустический интервал, равный 1 (т.е. тривиальный интервал), октавой - 2, чистой квинтой – 3/2, чистой квартой – 4/3. Интервал, не превосходящий 2, называется простым, больший 2 – составным. Обращением интервала λ называется величина 2/λ. При построении музыкального звукоряда используются октавы и квинты. Объяснение этому можно искать, например, в теории обертонов.

Биологические основы звука.
Поскольку нас интересуют не колебания вообще, а лишь воспринимаемые слухом человека, то следует ввести здесь определенные ограничения.

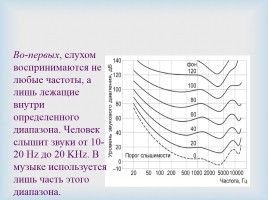
Во-первых, слухом воспринимаются не любые частоты, а лишь лежащие внутри определенного диапазона. Человек слышит звуки от 10-20 Hz до 20 KHz. В музыке используется лишь часть этого диапазона.

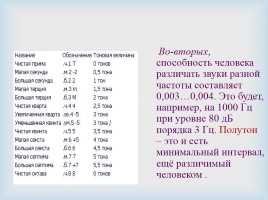
Во-вторых, способность человека различать звуки разной частоты составляет 0,003…0,004. Это будет, например, на 1000 Гц при уровне 80 дБ порядка 3 Гц. Полутон – это и есть минимальный интервал, ещё различимый человеком .

В-третьих, лишь меньшинство людей обладают абсолютным слухом, т.е. способны различать звуки по их частоте. Большинство же способны различать лишь интервалы между звуками, т.е. обладают относительным слухом.

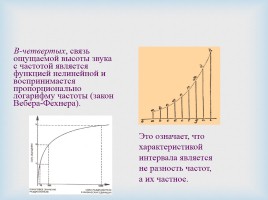
В-четвертых, связь ощущаемой высоты звука с частотой является функцией нелинейной и воспринимается пропорционально логарифму частоты (закон Вебера-Фехнера).
Это означает, что характеристикой интервала является не разность частот, а их частное.

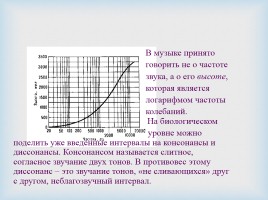
В музыке принято говорить не о частоте звука, а о его высоте, которая является логарифмом частоты колебаний. На биологическом уровне можно поделить уже введенные интервалы на консонансы и диссонансы. Консонансом называется слитное, согласное звучание двух тонов. В противовес этому диссонанс – это звучание тонов, «не сливающихся» друг с другом, неблагозвучный интервал.

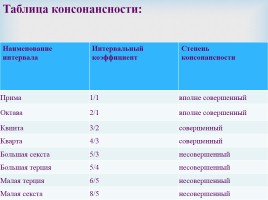
Наименование интервала  Интервальный коэффициент  Степень консонансности
Прима 1/1 вполне совершенный
Октава 2/1 вполне совершенный
Квинта 3/2 совершенный
Кварта 4/3 совершенный
Большая секста 5/3 несовершенный
Большая терция 5/4 несовершенный
Малая терция 6/5 несовершенный
Малая секста 8/5 несовершенный
Таблица консонансности:

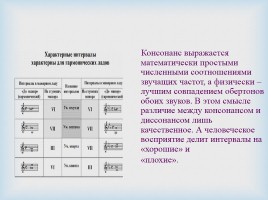
Консонанс выражается математически простыми численными соотношениями звучащих частот, а физически – лучшим совпадением обертонов обоих звуков. В этом смысле различие между консонансом и диссонансом лишь качественное. А человеческое восприятие делит интервалы на «хорошие» и «плохие».                     

О соотношении математического обоснования и психологического воздействия музыки.
"Звук за звуком", таково название стихотворения Йозефа фон Эйхендорфа; Штефану Георгу казалось, будто он сочиняет стихи как музыку, при этом он утверждал, что ценность поэзии определяется лишь формой того волнующего, что заключено в размере и звуке.
Абстрактная живопись является порождением движения, начавшегося примерно в 1800 году, его целью была музыкализация изобразительного искусства и поэзии; это движение ототвинуло на второй план специфику отдельных жанров искусств ради общих структурных свойств, позволивших провести аналогию с музыкальными явлениями.

Предпосылкой для возможного обобщения музыки явилось высказанная однажды Карлом Филиппом
Моритцем идея, что искусство представляет космос и поэтому является автономным.

Музыка - звучащее тождество вечной гармонии. "Музыкальные соотношения являются собственно основными соотношениями в природе".
Эта точка зрения Новалиса полностью совпала с лекциями Шеллинга по философии и искусству (1802-1803 гг.), где он утверждал: "В солнечной системе также отражается вся система музыки".

В связи с вопросом о соотношении рациональности и аффекта не столь важно уточнять исторические корни этого понятия музыки, сколько проверить совпадение с другими точками зрения, что может показать в некоторой степени ту сложную изменчивость, которая делает музыку, с одной стороны, абстрактно-логично действующим, а с другой стороны, самым эмоциональным видом искусства.

Лежащая в основе музыки система регулируется числовым порядком, причем простые числовые соотношения занимали особое место.
Они не только регулировали образование тетрахордов и тональностей, но представляли собой всеподчиняющий метафизический принцип, который позволял проводить любые аналогии.

Попытку описать движение планет, принимая во внимание музыкальные пропорции, как это пытался сделать еще Кеплер в 1610 г., следует отнести к античным временам, хотя уже Аристотель оспаривал, что небесная музыка по-настоящему звучит. Обоснование музыки с помощью числа в средние века, когда умение Пифагора продолжал развивать в основном Боэций, возвело занятие музыкой в абстракцию, так как реально звучащая музыка считалась неинтересной, но наряду с этим признавалась возможность научного подхода к понятию ее сущности.  

Практически заниматься музыкой, как и столярным ремеслом, считалось ars faciendi, т.е. этим искусством мог овладеть каждый, освоивший сумму тезисов. Музыка, одно из семи видов искусств, входила в квадривиум наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.

Музыка представляла содержание, доступное лишь уму, т.е. связанное с чисто умственной деятельностью, и в отличие от арифметики охватывала не устойчивые, а подвижные числовые отношения. Искусственное в музыке проявлялось в методе вычислений (например, определение консонанса).

На основе того, что музыке можно было найти чисто теоретическое математическое определение, она представлялась вплетенной во всю Вселенную. "Musica instrumentalis" — непосредственно звучащая музыка, была отображением "musica mundana" — гармонии мира, а "musica humana" — упорядоченных пропорций человеческого тела. Созерцательное погружение в математическую структуру звуковой системы привело к небесной механике.

Идея системного порядка, в которой сравниваются музыкальные отношения гармонии с земными, все вновь и вновь появляется в эстетических воззрениях.

И в очень разных, отдаленных большими промежутками времени культурных связях, пытались выразить эти гармонии постоянными числами с целью показать, что логика математики объясняет логику мира и в том числе музыки.

Так как в древние времена и в средние века предпола- гали, что человеческие органы подчиняются тем же принципам, что и музыка, было легко создать теорию о воздействиях, которая очень точно определяла структуру аффекта, например в сфере тональности, в зависимости от пропорций.

Важность этой теории подтверждается дискуссией о выразительности тональностей в тональной музыке. И так как числа понимались не как математический, а как метафизический принцип, их можно было считать предваряющими эмоциональное воздействие. Однако по мере того как такие убеждения ослабевали, musica humana и istrumentalis уже не соотносили с musica mundana,
отождествление пропорций и эмоционального воздействия стало проблематичным до такой степени, что в XX в. музыка в своих эстетических намерениях дошла до чистого расчета и не могла уже ни выражать аффекта, ни вызывать его.

И именно музыка, которая оказывала самые интенсивные эмоциональные воздействия, музыка XIX в., хотя еще и рассматривалась как система совершенных отношений, однако эта система уже больше не объясняла психологического воздействия, а наоборот, ее обоснованием служили психологические данные.

Музыка периода классицизма и романтизма уже почти не могла объяснить логическое действие взаимосвязей простыми математическими пропорциями. Даже трезвучие в темперированной системе, явившееся предпосылкой для развития инструментальной музыки, считалось очень смелой заявкой. Характер этой музыки как тождества рационального порядка определялся чувством хорошо взвешенной гармонии и симметрическими группировками, т.е. в отличие от античных смен рациональность звуковой системы обосновывалась аффектом.

Музыкальная логика — Иоганн Николаус Форкель использовал в 1788 г. это выражение впервые как осмысление взаимосвязей и отношений. А сложные отношения, которые воспринимались в то же время как выражение совершенного порядка , представляли музыку как метафору вселенной.

Музыкальная звуковая система не могла быть порождением какой-либо другой, в том числе и математической системы, а наоборот, другие системы были заимствованы у музыки.

И какие бы параллели ни проводились между абстрактным понятием музыки периода романтизма и более ранними и поздними периодами, с идеей абсолютной музыки исчез и принцип, который объяснял ее эмоциональное воздействие и ставил аффекты в зависимость от рациональности.

Высказывания знаменитостей.
«Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства её должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.» (Плутарх)

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришёл к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и что между ними размещается всё, что человечество создало в области науки и искусства.» (Генрих Нейгауз)

Настоящая наука и настоящая музыка требуют однородного   мыслительного процесса. (Альберт Эйнштейн)

Вывод:
Математика является ключом к тайнам мировоззрения. Использование   математической теории музыки позволяет создавать особую музыку, которая сдерживает и исцеляет болезни, обращает и приводит душевные страсти в спокойное состояние. Сравнивая музыку и математику, мы делаем вывод, что математика, как наука, может развиваться без музыки. А музыка как искусство подчиняется многим законам математики и не может существовать без неё. Искусство надо принимать сердцем, душой и служить ему , но тем не менее, если мы попытаемся приложить математику к какой–то области искусства, то наша попытка , скорее всего, увенчается успехом.

1.И.Г.Зенгевич «Эстетика урока математики» - М. «Просвещение»,1981 2. Л.С. Сагателова, В.Н. Студеницкая «Геометрия:красота и гармония» - Волгоград: учитель, 2007 3.Энциклопедический словарь юного математика – 1989 4.Введение в математическое моделирование. Учебное пособие. Под ред. П.В. Трусова – М. «Логос»,2007 5. http://festival.1september.ru/articles/583335/ 6.images.yandex.ru
Использованные материалы: