Презентация - Решение задач по теме: «Первый признак равенства треугольников»

Решение задач по теме: «Первый признак равенства треугольников» 7 класс

Цели и задачи: Повторить понятие треугольника, его элементов, понятие равных фигур, первый признак равенства треугольников. Учиться решать задачи на применение первого признака равенства треугольников.

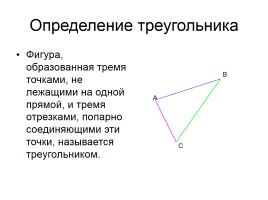
Определение треугольника
Фигура, образованная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки, называется треугольником.
В
С
А

Равенство геометрических фигур
Геометрические фигуры называют равными, если при наложении они совпадают.

Равные фигуры

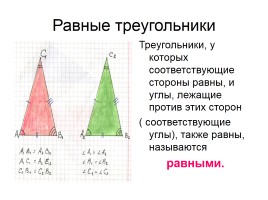
Равные треугольники
Треугольники, у которых соответствующие стороны равны, и углы, лежащие против этих сторон ( соответствующие углы), также равны, называются равными.

Давай подумаем

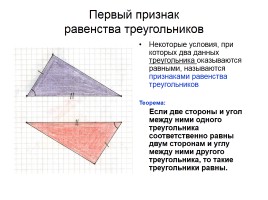
Первый признак равенства треугольников
Некоторые условия, при которых два данных треугольника оказываются равными, называются признаками равенства треугольников Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Решение задач
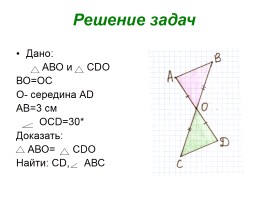
Дано: АВО и СDО ВО=ОС О- середина АD АВ=3 см ОСD=30* Доказать: АВО= СDО Найти: СD, АВС

Доказательство:
АОВ= СОD (как вертикальные), АО=ОD( так как О - середина АD), ВО=ОС (по условию) АОВ= СОD (по I признаку равенства треугольников) Ч.Т.Д.

Решение
Так как треугольники равны, равны их соответствующие элементы Т.о. СD=АВ=3 см АВС= ОСD=30* Ответ: 3 см, 30*

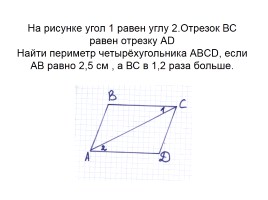
На рисунке угол 1 равен углу 2.Отрезок ВС равен отрезку АD Найти периметр четырёхугольника АBСD, если АВ равно 2,5 см , а ВС в 1,2 раза больше.

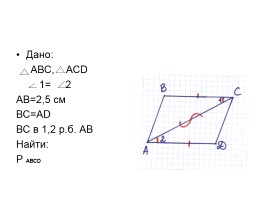
Дано: АВС, АСD 1= 2 АВ=2,5 см ВС=АD ВС в 1,2 р.б. АВ Найти: Р АВСD

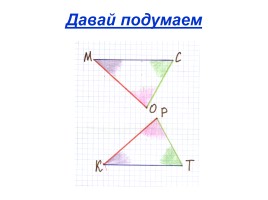
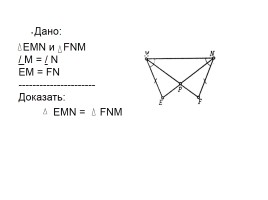
Дано:
EMN и FNM / М = / N EM = FN ---------------------- Доказать:
EMN = FNM

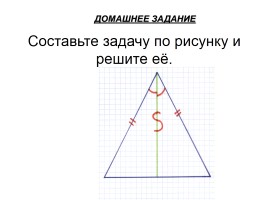
Составьте задачу по рисунку и решите её.
ДОМАШНЕЕ ЗАДАНИЕ