Презентация - Урок №11 «Сравнение отрезков - Длина отрезков»

Тема урока: Сравнение отрезков. Длина отрезков.
УРОК № 11
Цели урока: Провести анализ самостоятельной работы. Повторить определение, построение и обозначение отрезка Объяснить правило сравнения отрезков, ввести понятие середины

Выполнить последовательно задания: 1. Построить прямую АВ, и отрезок CD, пересекающиеся в точке B. 2. Построить прямую a и отрезок NM таким образом, чтобы они не пересекались. И построить луч NK, пересекающий прямую а. Пересечет ли луч отрезок?

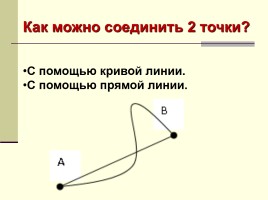
Как можно соединить 2 точки? С помощью кривой линии. С помощью прямой линии.

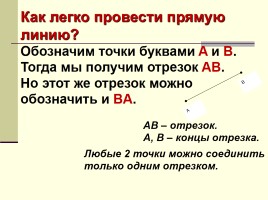
AB – отрезок. A, B – концы отрезка.
Любые 2 точки можно соединить только одним отрезком.
Как легко провести прямую линию? Обозначим точки буквами A и B. Тогда мы получим отрезок AB. Но этот же отрезок можно обозначить и BA.

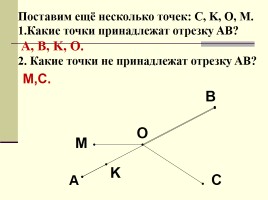
Поставим ещё несколько точек: C, K, O, M. Какие точки принадлежат отрезку AB? A, B, K, O. 2. Какие точки не принадлежат отрезку AB?
М,С.

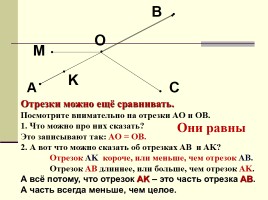
Отрезки можно ещё сравнивать. Посмотрите внимательно на отрезки AO и OB. 1. Что можно про них сказать? Это записывают так: AO = OB. 2. А вот что можно сказать об отрезках AB и AK? Отрезок AK короче, или меньше, чем отрезок AB. Отрезок AB длиннее, или больше, чем отрезок AK. А всё потому, что отрезок AK – это часть отрезка AB. А часть всегда меньше, чем целое.
Они равны

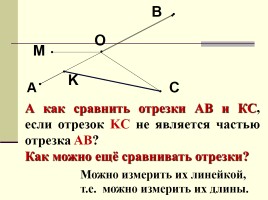
А как сравнить отрезки AB и КС, если отрезок KC не является частью отрезка AB? Как можно ещё сравнивать отрезки?
Можно измерить их линейкой, т.е. можно измерить их длины.

Начертить отрезок АВ, длина отрезка AB равна – 5 см. Записывают так: AB = 5 см.
10 см = 1 дм 100 см = 1 м 1 см = 10 мм 1 км = 1000 м
А какие ещё единицы измерения длины вы знаете? Давайте вспомним, как одни единицы длины выражаются через другие:

№ 88, 91(а,г), 92, 93 (а,г)

№ 90
Вывод: Длина отрезка – это число, которое показывает, сколько раз отрезок, длина которого принята за единицу (меру) длины, укладывается в измерительном отрезке.

Ответить на вопросы: 1. Сколько прямых можно провести через одну точку? 2.Чем отличается изображение луча от изображения отрезка? 3. Назовите точку, являющуюся началом луча СD? 4. Сколько общих точек могут иметь две прямые?

Домашнее задание.
§ 5, выучить правила, № 89, 91 (б,в), 93 (б,в)
Спасибо за урок!