Презентация - Тренажер «Чтение» графиков
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 81%
- Слайдов: 25
- Просмотров: 3171
- Скачиваний: 1134
- Размер: 0.53 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Кроссворд - тренажёр по литературному чтению (3класс , программа Л.В.Занкова)
Кроссворд - тренажёр по литературному чтению (3класс , программа Л.В.Занкова) Тренажёр учимся читать предшкольная подготовка, литературное чтение
Тренажёр учимся читать предшкольная подготовка, литературное чтение Тренажер: техника чтения. 4 часть
Тренажер: техника чтения. 4 часть Тренажер: техника чтения. 2 часть
Тренажер: техника чтения. 2 часть Тренажер: техника чтения. 1 часть
Тренажер: техника чтения. 1 часть О братьях наших меньших. Тест-тренажёр. Литературное чтение 1 класс УМК «школа России»
О братьях наших меньших. Тест-тренажёр. Литературное чтение 1 класс УМК «школа России» «Я и мои друзья». Тест-тренажёр. Литературное чтение 1 класс
«Я и мои друзья». Тест-тренажёр. Литературное чтение 1 класс
Слайды и текст этой онлайн презентации
Слайд 1

Тренажер.
«Чтение» графиков Программа составлена по КИМ ЕГЭ.
«Чтение» графиков Программа составлена по КИМ ЕГЭ.
Слайд 2
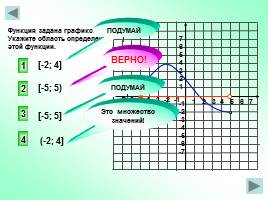
Функция задана графиком.
Укажите область определения
этой функции.
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
[-2; 4]
[-5; 5)
[-5; 5]
(-2; 4]
2
1
3
4
ПОДУМАЙ!
ВЕРНО!
Это множество значений!
ПОДУМАЙ!
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
[-2; 4]
[-5; 5)
[-5; 5]
(-2; 4]
2
1
3
4
ПОДУМАЙ!
ВЕРНО!
Это множество значений!
ПОДУМАЙ!
Слайд 3
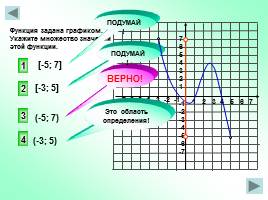
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите множество значений этой функции.
[-5; 7]
(-5; 7)
[-3; 5]
(-3; 5)
3
ВЕРНО!
1
2
4
Это область определения!
ПОДУМАЙ!
ПОДУМАЙ!
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите множество значений этой функции.
[-5; 7]
(-5; 7)
[-3; 5]
(-3; 5)
3
ВЕРНО!
1
2
4
Это область определения!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 4
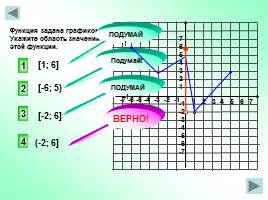
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите область значений этой функции.
[1; 6]
[-6; 5)
[-2; 6]
(-2; 6]
4
ВЕРНО!
1
3
2
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите область значений этой функции.
[1; 6]
[-6; 5)
[-2; 6]
(-2; 6]
4
ВЕРНО!
1
3
2
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 5
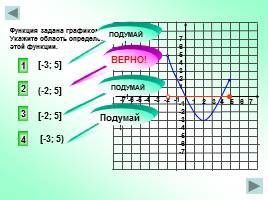
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите область определения этой функции.
[-3; 5]
[-3; 5)
[-2; 5]
(-2; 5]
2
ВЕРНО!
1
3
4
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите область определения этой функции.
[-3; 5]
[-3; 5)
[-2; 5]
(-2; 5]
2
ВЕРНО!
1
3
4
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 6
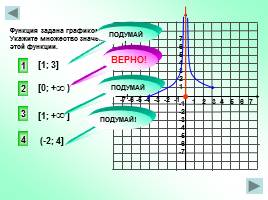
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком на [-4;0) (0;3]. Укажите множество значений этой функции.
[1; 3]
[0; + )
[1; + ]
(-2; 4]
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком на [-4;0) (0;3]. Укажите множество значений этой функции.
[1; 3]
[0; + )
[1; + ]
(-2; 4]
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 7
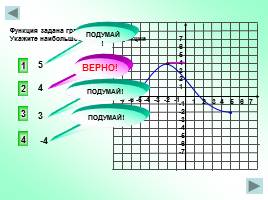
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите наибольшее значение функции
5
4
3
-4
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
-7 -6 -5 -4 -3 -2 -1
7 6 5 4 3 2 1
-1 -2 -3 -4 -5 -6 -7
Функция задана графиком. Укажите наибольшее значение функции
5
4
3
-4
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 8
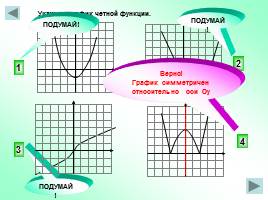
Укажите график четной функции.
4
2
3
1
ПОДУМАЙ!
ПОДУМАЙ!
Верно! График симметричен относительно оси Оу
ПОДУМАЙ!
4
2
3
1
ПОДУМАЙ!
ПОДУМАЙ!
Верно! График симметричен относительно оси Оу
ПОДУМАЙ!
Слайд 9
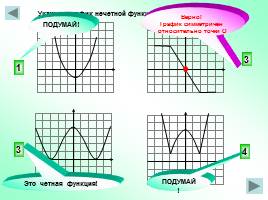
Укажите график нечетной функции.
3
4
3
1
ПОДУМАЙ!
Это четная функция!
ПОДУМАЙ!
Верно! График симметричен относительно точки О
3
4
3
1
ПОДУМАЙ!
Это четная функция!
ПОДУМАЙ!
Верно! График симметричен относительно точки О
Слайд 10
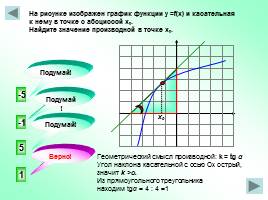
На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной в точке х0.
1
-1
5
-5
Подумай!
Подумай!
Верно!
Подумай!
х0
Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох острый, значит k >o. Из прямоугольного треугольника находим tgα = 4 : 4 =1
Слайд 11
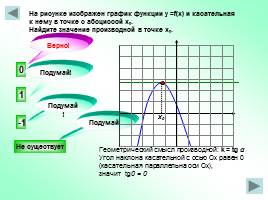
На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
0
-1
Не существует
1
Подумай!
Подумай!
Верно!
Подумай!
х0
Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох равен 0 (касательная параллельна оси Ох), значит tg0 = 0
0
-1
Не существует
1
Подумай!
Подумай!
Верно!
Подумай!
х0
Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох равен 0 (касательная параллельна оси Ох), значит tg0 = 0
Слайд 12
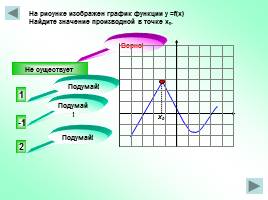
На рисунке изображен график функции у =f(x)
Найдите значение производной в точке х0.
Не существует
-1
2
1
Подумай!
Подумай!
Верно!
Подумай!
х0
Не существует
-1
2
1
Подумай!
Подумай!
Верно!
Подумай!
х0
Слайд 13
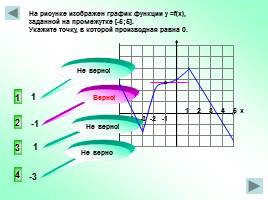
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку, в которой производная равна 0.
2
3
4
1
Не верно!
Не верно
Верно!
Не верно!
1
-1
1
-3
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку, в которой производная равна 0.
2
3
4
1
Не верно!
Не верно
Верно!
Не верно!
1
-1
1
-3
Слайд 14
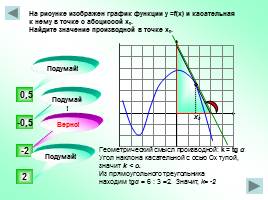
На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
-2
-0,5
2
0,5
Подумай!
Подумай!
Верно!
Подумай!
х0
Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох тупой, значит k < o. Из прямоугольного треугольника находим tgα = 6 : 3 =2. Значит, k= -2
-2
-0,5
2
0,5
Подумай!
Подумай!
Верно!
Подумай!
х0
Геометрический смысл производной: k = tg α Угол наклона касательной с осью Ох тупой, значит k < o. Из прямоугольного треугольника находим tgα = 6 : 3 =2. Значит, k= -2
Слайд 15
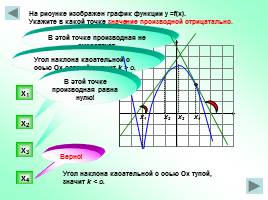
На рисунке изображен график функции у =f(x).
Укажите в какой точке значение производной отрицатально.
х4
х2
х3
В этой точке производная не существует
Верно!
Угол наклона касательной с осью Ох острый, значит k > o.
х1 х2 х3 х4
Угол наклона касательной с осью Ох тупой, значит k < o.
х1
В этой точке производная равна нулю!
х4
х2
х3
В этой точке производная не существует
Верно!
Угол наклона касательной с осью Ох острый, значит k > o.
х1 х2 х3 х4
Угол наклона касательной с осью Ох тупой, значит k < o.
х1
В этой точке производная равна нулю!
Слайд 16
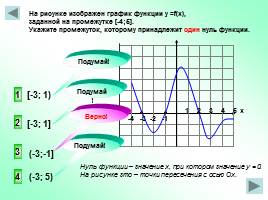
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежит один нуль функции.
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
[-3; 1)
[-3; 1]
(-3;-1]
(-3; 5)
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежит один нуль функции.
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
[-3; 1)
[-3; 1]
(-3;-1]
(-3; 5)
Слайд 17
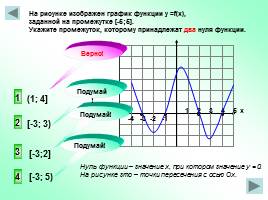
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат два нуля функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
(1; 4]
[-3; 3)
[-3;2]
[-3; 5)
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат два нуля функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
(1; 4]
[-3; 3)
[-3;2]
[-3; 5)
Слайд 18
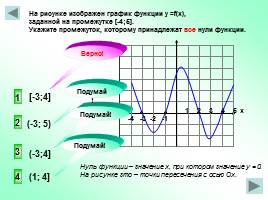
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежат все нули функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
(1; 4]
(-3; 5)
(-3;4]
[-3;4]
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежат все нули функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
(1; 4]
(-3; 5)
(-3;4]
[-3;4]
Слайд 19
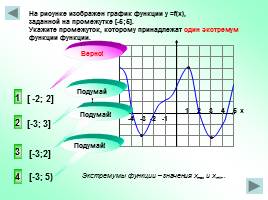
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат один экстремум функции функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Экстремумы функции – значения xmax и xmin..
[ -2; 2]
[-3; 3]
[-3;2]
[-3; 5)
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат один экстремум функции функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Экстремумы функции – значения xmax и xmin..
[ -2; 2]
[-3; 3]
[-3;2]
[-3; 5)
Слайд 20
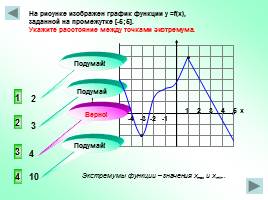
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите расстояние между точками экстремума.
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
Экстремумы функции – значения xmax и xmin..
2
3
4
10
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите расстояние между точками экстремума.
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
Экстремумы функции – значения xmax и xmin..
2
3
4
10
Слайд 21
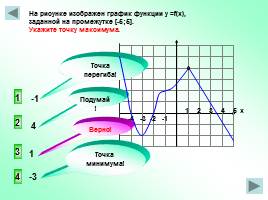
-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку максимума.
3
2
4
1
Точка перегиба!
Точка минимума!
Верно!
Подумай!
-1
4
1
-3
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку максимума.
3
2
4
1
Точка перегиба!
Точка минимума!
Верно!
Подумай!
-1
4
1
-3
Слайд 22
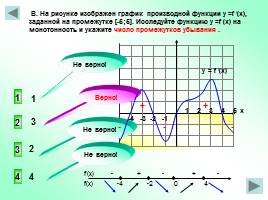
-4 -3 -2 -1
1 2 3 4 5 х
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число промежутков убывания .
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
1
3
2
4
y = f /(x)
+ + - - -
1 2 3 4 5 х
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число промежутков убывания .
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
1
3
2
4
y = f /(x)
+ + - - -
Слайд 23
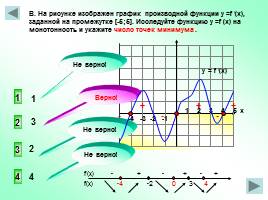
-4 -3 -2 -1
1 2 3 4 5 х
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число точек минимума .
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
1
3
2
4
y = f /(x)
+ + + - - -
1 2 3 4 5 х
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число точек минимума .
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
1
3
2
4
y = f /(x)
+ + + - - -
Слайд 24
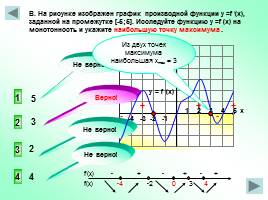
-4 -3 -2 -1
1 2 3 4 5 х
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите наибольшую точку максимума .
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
5
3
2
4
y = f /(x)
+ + + - - -
Из двух точек максимума наибольшая хmax = 3
1 2 3 4 5 х
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите наибольшую точку максимума .
2
3
4
1
Не верно!
Не верно!
Верно!
Не верно!
5
3
2
4
y = f /(x)
+ + + - - -
Из двух точек максимума наибольшая хmax = 3
Слайд 25
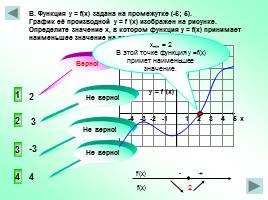
-4 -3 -2 -1
1 2 3 4 5 х
В. Функция y = f(x) задана на промежутке (-5; 5). График её производной y = f /(x) изображен на рисунке. Определите значение х, в котором функция у = f(x) принимает наименьшее значение на промежутке ( -5; 5).
1
3
4
2
Не верно!
Не верно!
Верно!
Не верно!
2
3
-3
4
y = f /(x)
хmin = 2 В этой точке функция у =f(x) примет наименьшее значение.
1 2 3 4 5 х
В. Функция y = f(x) задана на промежутке (-5; 5). График её производной y = f /(x) изображен на рисунке. Определите значение х, в котором функция у = f(x) принимает наименьшее значение на промежутке ( -5; 5).
1
3
4
2
Не верно!
Не верно!
Верно!
Не верно!
2
3
-3
4
y = f /(x)
хmin = 2 В этой точке функция у =f(x) примет наименьшее значение.
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
