Презентация - Неоптолемеевская механика

Неоптолемеевская механика механика эры космоса
Карбушев Максим

2
Небит-Даг – Москва 1978 - 1995

Неоптолемеевская механика - это не новая механика, а новый язык механики на фундаменте ньютоновской. Аналогично механикам Лагранжа,, Гамильтона и т.п. Разработана применительно к задачам мегамеханики – небесной, звездной, галактической, космологической и космонавтики. Для космонавтики коперникианский подход рассмотрения движения в системе Солнца или, вообще, выделенных системах отсчета несодержателен. В ней необходимо рассматривать движение всех объектов – Солнца, Земли, астероидов и метеоритов, планет и лун, иных космических объектов в системе отсчета космического корабля. Фактически, речь идет о возврате к птолемеевскому подходу в механике. Для создания неоптолемеевского языка требуется новый анализ основных механических понятий, исходя из практики космонавтики (!!!!!)

Понятие о механическом состоянии механических объектов
Механическое состояние механических объектов – новое понятие механики. Рассматриваются два типа состояний – свободное и несвободное. Парашютист в свободном падении, снаряд или боеголовка, космический корабль, космонавт на орбите, Земля, Луна, Солнце, звезды, галактики, рассматриваемые как элементарные механические объекты (ЭМО) – примеры объектов в свободном механическом состоянии. Человек или иной предмет на поверхности или внутри Земли, объект на Луне и Солнце, КК и космонавт в нем на активном участке траектории или на орбите при учете «негравитационного торможения», электрон в атоме, частицы солнечного ветра в магнитосфере Земли –примеры объектов в несвободном механическом состоянии.

Весомость как характеристика и мера несвободного механического состояния
Источник несвободы в механике называется силой. В языке Ньютона именно сила является фундаментальным, первичным, неопределяемым понятием. Для Ньютона сила ассоциировалась с мышцей и тетивой. В третьей механике в качестве фундаментального понятия принимается характеристика механического состояния, называемая ВЕСОМОСТЬЮ. Весомость есть вектор, приложенный к самому телу. Свободные механические объекты находятся в невесомости, т.е. в имеют нулевую весомость. Несвободные объекты находятся в весомом состоянии с ненулевой весомостью. Устройство для измерения весомости называется ВЕСОМОМЕТР. Весомометрическими устройствами или индикаторами обладают почти все живые организмы. В вестибулярном аппарате целый набор весомометров Это шестой орган чувств. Простейший весомометр представляет грузик с пружинкой. Это широко используемый прибор, называемый сейчас (неверно) акселерометром или гравиметром (это вернее) или ньютонометром (тоже неверно).
F
W
весомометр
А еще нелепее – перегрузометр.

Весомика
В системе СИ весомость измеряется в Н/кг. Называется «Галилео» - Гл. Земная весомость 9.81 Гл, лунная – 1.6 Гл, солнечная – 27 Гл. Весомость может быть постоянной и переменной, изменяться по величине (болтанка, тряска) или по направлению (качка), быть однородной в пространстве и неоднородной. Новый раздел механики – весомика. Это наука о механическом состоянии объектов. Планетная весомика, земная весомика (гравиметрия), космическая и авиационная весомики. Весомика развлечений для парковых аттракционов. Весомика при прочностных расчетах и конструировании космических, авиационных, морских и иных транспортных аппаратов, в ТММ она широко используется под некорректными именами.Медицинская и ветеринарная весомики. И т.д. Метрология весомости есть база вообще всей метрологии. Ибо сила эталонируется через весомость и массу. Весомика один из важнейших разделов механики, значение которой трудно переоценить. Ее пока нет так как нет терминологии. Это уже первый плод нового языка механики. Сейчас в этой области используется нечто типа «перегрузка», «недогрузка», «недоперегрузка» (а что такое «грузка»?), «собственное ускорение» (а это что?). Невнятность языка обуславливает невнятность мысли и невозможность существования науки. Четкость языка есть ясность мысли и дает эффективную науку и практику.

Понятие механического пространства
Механическое пространство –сцена, на которой играется пьеса механики. Перенос практической деятельности человека в космическое пространство требует переосмысления этого понятия. Ведь в космосе нет дорог, городов, островов, континентов, гор и т.д., нет географических карт. В нем все подвижно и динамично. Возникает новая наука – геометрика, которая создает базу геометриизации космического пространства. Главное понятие геометрики –понятие системы отсчета. Но предварительно надо ввести главные типы механических объектов. Это элементарный механический объект (ЭМО), механическое тело (МТ) и механическая среда (МС). МТ может быть разделено на ЭМО, МС на отдельные тела и далее на ЭМО. Система отсчета это прежде всего механическая среда. Ее описание содержится в описании состояний элементов и их взаимосвязей. Вводится понятие абсолютно жесткой связи и прямой как образа напряженной гибкой струны (но не луча света). Абсолютно жесткая среда –среда, между элементами которой существует абсолютно жесткая связь. Системы отсчета на абсолютно жестких средах это ньютоновские системы отсчета. В используются и неньютоновские системы отсчета. Система координат – совокупность чисел, приписанных элементам отсчета. На одной системе (тел) отсчета можно ввести множество систем координат (декартову, полярную, сферическую и т.д.).

Понятие механического пространства (продолжение)
Среда, выполненная свободными, невесомыми элементами, называется абсолютно мягкой. Система отсчета на абсолютно мягких средах называется мягкой системой отсчета. Мягкая ньютоновская система отсчета (одновременно и мягкая, и жесткая) называется инерциальной системой отсчета. Для инерциальных систем отсчета справедлив принцип Галилея: свободное (невесомое) тело движется в ней равномерно и прямолинейно Пространство, в котором можно ввести инерциальную систему отсчета, называется галилеевым. Иные пространства называются негалилеевыми. Распределение весомости элементов среды (в ньютоновской системе отсчета) создает весомостное поле негалилеевой системы отсчета. Исчисление времени. Идеальные часы. Часы, на ход которые не влияют никакие механические воздействия: Если такие часы синхронизировать в одном месте, а затем их произвольно бросать, кидать, вращать, возить в любое место, то после возврата в одно место и остановки друг относительно друга их показания совпадут. Часы размещаются только у наблюдателя. Координатное время определяется законами движения тел. И если предсказания теории и наблюдения совпадают, то и координатное время исчислено верно.

Что такое гравитация
Гравитация заключается в существовании в окрестности тел области негалилеевости. Гравитация не взаимодействие, а свойство. Его можно изменить исключительно воздействием на источник гравитации.. Носителем свойства является пространство. Гравитация не меняет свободы и невесомости. Проявление этого свойства состоит в том, что свободные тела в нем не двигаются равномерно и прямолинейно. Область пространства, в которой проявляется негалилеевость, называется гравитационным полем. На достаточном удалении от источника гравитации поле шарообразно и топологически открыто. Величина, пропорциональная квадрату радиуса области негалилеевости объекта характеризует имманентное свойство объекта, называемое массой.. Система отсчета, асимптотически инерциальная на бесконечности, называется гармонической. Поле весомости в гармонической системе отсчета является собственно гравитационным полем. Общее весомостное поле аддитивно и состоит из собственно гравитационного поля и поля весомости неинерциальной системы отсчета без учета гравитации (например, связанного с вращением системы отсчета или реактивного воздействия). Локально эти поля неразделимы (принцип Эйнштейна).

Фундамент механики построен. Начинаем построение самой механики

Аксиоматика
Определение силы: F – сила, W – весомость. В новой механике нет гравитационных сил. Все макросилы в ней имеют электромагнитный характер. Например, тело на поверхности Земли имеет весомость, направленную вниз. В нему приложена сила, направленная вверх. Это сила упругости опоры. Она является электромагнитной. Закон (аксиома) взаимодействия (третий закон Ньютона) : . Уравнение движения в инерциальной системе отсчета (второй закон (аксиома) Ньютона): W – весомость, w – ускорение.

Основные законы
Полевые уравнения (уравнения поля весомости) Здесь V(r) – полевая весомость. U – весомость гравитационная, H –весомость, связанная с неинерциальностью системы отсчета. - угловая скорость вращения системы отсчета,  - плотность. Начальные условия: V0 = W(r = 0). В этом принципиальное отличие от уравнений электромагнитного поля, в которых задаются граничные условия. Почему волн гравитационной или неинерциальной весомости не существует? Уравнение движения произвольного тела в произвольной (ньютоновской) системе отсчета в произвольном пространстве Это универсальное уравнение движения, так как в него не входят никакие собственные, имманентные характеристики тела.

Наконец, закон сохранения массы (уравнение неразрывности): Все понятия и законы новой механики сформулированы. Они полностью вытекают из ньютоновской механики. Метод динамических систем отсчета состоит в использования систем отсчета, характеристики которых являются переменными задачи.
Ориентация систем отсчета в задачах 1, 2, 3 и 4-х тел. Характеристиками системы отсчета являются угловая скорость вращения (t) и весомость начала системы отсчета W0(t).

Уравнение поля весомости в неинерциальной системе отсчета
Уравнение гравитационного поля ансамбля n+1 свободных тел на самих телах (начало системы отсчета на нулевом теле, U0=0).
Расходимостей и бесконечностей нет. Полное развернутое уравнение движения
Остальные компоненты получаются циклической перестановкой. Оно сложнее ньютоновского F=ma, но его возможности потрясают.

Простейшие задачи Земля в системе отчета космического корабля. Ось Ох направляем на центр Земли. Ищем статическое решение на удалении x центра Земли от ККс постоянной угловой скоростью системы отсчета. Центр Земли и КК невесомы. Согласно уравнениям движения имеем
Х
О
KK
Земля
x
Общая задача двух гравитирующих тел. Нулевое тело - начало отсчета. Движение одномерно, размерность – 2, ранг – 3.
Решение – коническое сечение с параметром - сумма масс. Существует прецессирующее решение.

Задача трех тел. Одно движение одномерно, второе – двухмерно. Размерность 6, ранг 8.

Точные решения в задаче многих тел, найденные в НПМ В задаче двух тел все решения аналитические. Дополнительно обнаружено решение в прецессирующей системе отсчета. Реальное подтверждение – прецессия Солнечной системы. Коллинеарные решения во вращающейся и прецессирующей системе любого количества тел. Плоская задача трех тел тел произвольной массы во вращающейся системе отсчета в конфигурации правильного неподвижного или подвижного треугольника. Плоская задача произвольного количества тел одинаковой массы в конфигурации неподвижного или подвижного правильного многоугольника во вращающейся системе отсчета. Пространственная задача четырех тел произвольной массы в невращающейся системе отсчета в конфигурации подвижного правильного тетраэдра. Пространственная задача 6, 8, 12 и 20 тел одинаковой массы в невращающейся системе отсчета в конфигурации подвижного правильного многогранника.

Новый класс механических объектов – росцилляторы Росциллятор (ротатор-осциллятор) есть совокупность элементов, соединенных упругими связями, которая одновременно может участвовать во вращательном движении. Взаимодействие вращательных и колебательных степеней свободы приводит к интересным эффектам – замораживанию тех или иных колебательных степеней свободы при некоторых скоростях вращения. Образом осциллятора является молекула. Замораживание степеней свободы приводит как бы к изменению степеней свободы и соответственно к изменению теплоемкости. Это можно также описать как появление антирезонансов или полос прозрачности.
Простейший осциллятор – двухчастичный осциллятор, обладающий пространственной свободой. У него имеется только одна антирезонансная скорость вращения. У многочастичных росцилляторов может быть несколько антирезонансных скоростей.

Однородные нестационарные среды
Однородные среды первого класса. Это газ, жидкость, твердая среда. Их свойство однородность, одинаковость всех характеристик во всех ее местах. Однородные среды второго класса: среды, которые описываются одинаково с точки зрения любого наблюдателя, связанного со средой. Эти среды нестационарные ОНС. Критерии ОНС:
Однородность плотности среды. Она не зависит от расстояния, но может меняться со временем. Пропорциональность скорости движения элементов среды расстоянию H назовем хаблианом. H=H(t). Отсутствие взаимодействия – невесомость элементов среды.
ОНС бывают негравитирующие (макроОНС) и гравитирующие (мегаОНС), вращающиеся и невращающиеся, изотропные и неизотропные, одно-, двух- и трехмерными, Это целый физический мир, очень богатый приложениями.

Однородные трехмерные гравитирующие нестационарные среды. Они экспериментально обнаружены Эдвином Хабблом и теоретически описаны английским астрофизиком, математиком и механиком Эдуардом Милном (1996-1950) в середине тридцатых годов.
Гравитирующий (мега) взрыв может быть необратимым и обратимым - среда после взрыва разлетается, затем. останавливается и вновь сжимается. Если постоянную Ньютона обратить в нуль, то получаем макровзрыв, взрыв обычного ВВ в космосе и вне гравитационного поля. Все частицы летят по инерции. Наибольшая скорость на фронте взрыва
r
v
Vf - скорость фронта
Распределение скоростей
w – удельное энерговыделение.

r
v
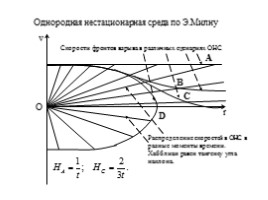
Скорости фронтов взрыва в различных сценариях ОНС
А
B
C
D
Распределение скоростей в ОНС в разные моменты времени. Хабблиан равен тангенсу угла наклона.
Однородная нестационарная среда по Э.Милну
О

Двухмерные ОНС
Существует частное стационарное состояние. Угловая скорость вращения связана со стационарной планарной плотностью:
- двухмерная плотность.  - угловая скорость. При =0 имеем макровзрыв вращающегося тела, например, маховика.
Модель галактики. При этом линейность окружной скорости соответствует данным. И отпадает потребность в «невидимых массах». Гипотеза: галактики происходят не акрецией рассеянного вещества, а взрывом массивных протогалактических образований.
Доказательство. Наша галактика имеет старую сферическую подсистему и молодую плоскую. Это доказательство взрывного происхождения нашей галактики, причем первый взрыв был трехмерным, а оставшийся керн, пришедший во вращение, взорвался по плоскому типу.

Одномерные ОНС
Взрыв идет вдоль оси Ох.  - линейная плотность. Прецессирующая система. Негравитирующий линейных взрыв показывает предел скорости пули или снаряда
Существует стационарное частное решение. Оно может стать моделью одномерной солнечной системы. Одновременно позволяет выдвинуть гипотезу происхождения Солнечной системы из линейный взрыва звезды в двойной звездной системе ее и Солнца. Это позволяет объяснить разнообразие планет, которые произошли из разных частей звезды. Например, наличие магнитного поля позволяет предположить, что Земля произошла из центральных частей звезды. А внешние части сложили Юпитер. На этом очень богатую тему однородных нестационарных сред завершаем.

Теоретическая космическая механика Новая неоптолемеевская механика специально «заточена» под задачи космонавтики. В существующем языке космический аппарат является объектом наблюдения. При этом используется большое количество «внешних» систем отсчета – система Земли, Солнца, Луны, объекта сближения и т.д. Результаты расчетов координаты, из которых еще надо извлечь требуемые данные с помощью «вычитательных» процедур, уменьшающих точность. Неоптолемеевский подход состоит в использовании системы отсчета КК, в которой рассматривается движение всех остальных космических объектов – Земли, Солнца, звезд, планет, Луны, объектов стыковки, угрожающих объектов и т.д. Эта система отсчета с единственным началом, но с возможностью иметь множество систем отсчета различных ориентацией в зависимости от объекта(ов) наблюдения. Расчеты прямо дают контролируемые или управляемые удаления и направления,.

Механика запуска. Рассмотрены задачи запуска. Предложены и проанализированы некоторые схемы, определяемые программами весомости W(t) и угла разворота (t). Введено понятие интегральной весомости P и к.п.д. K схемы запуска,
Рассмотрена задача нахождения схемы выведения, минимизирующей интегральную весомость, и нахождения орбиты, на которой достигается максимум к.п.д. Показано, что такой орбитой является орбита с высотой около 650 км и максимальный к.п.д. равен 0.725. Весомость равна 3.2 G (земной), а угол разворота двигателя 133. Возможно она окажется полезной в качестве к промежуточной при запуске на высокие и далекие орбиты. Рассмотрена схема двухстадийного запуска на круговую орбиту (с вертикальным стартом): первая стадия – выход на орбиту, вторая – орбитальный разгон до космической скорости. Думается, что теоретические предельные эффективности могут оказаться столь же полезными в космонавтике, как таковые же в термодинамике и теплоэнергетике.

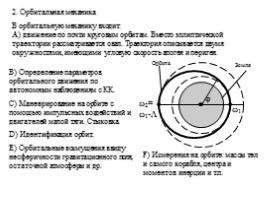
2. Орбитальная механика В орбитальную механику входит: А) движение по почти круговым орбитам. Вместо эллиптической траектории рассматривается овал. Траектория описывается двумя окружностями, имеющими угловую скорость апогея и перигея.
1
2= 1-

B) Определение параметров орбитального движения по автономным наблюдениям с КК. С) Маневрирование на орбите с помощью импульсных воздействий и двигателей малой тяги. Стыковка. D) Идентификация орбит. Е) Орбитальные возмущения ввиду несферичности гравитационного поля, остаточной атмосферы и др.
F) Измерения на орбите: массы тел и самого корабля, центра и моментов инерции и т.п.
Орбита
Земля

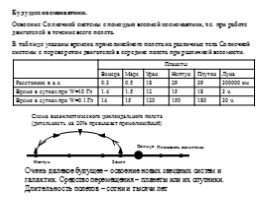
Будущее космонавтики. Освоение Солнечной системы с помощью весомой космонавтики, т.е. при работе двигателей в течение всего полета. В таблице указаны времена прямолинейного полета на различные тела Солнечной системы с переворотом двигателей в середине полета при различной весомости.
Планеты Планеты Планеты Планеты Планеты Планеты
Венера Марс Уран Нептун Плутон Луна
Расстояние в а.е. 0.3 0.5 18 29 39 300000 км
Время в сутках при W=10 Гл 1.4 1.5 12 15 18 3 ч.
Время в сутках при W=0.1 Гл 14 15 120 150 180 30 ч.
Солнце
Земля
Нептун
Плоскость эклиптики
Схема внеэклиптического циклоидального полета (дительность на 20% превышает прямолинейный)
Очень далекое будущее – освоение новых звездных систем и галактик. Средство перемещения – планеты или их спутники. Длительность полетов – сотни и тысячи лет

Заключение. Работа над новым языком механики велась более тридцати лет. Я являюсь учеником Ландау и Капицы. Но в силу определенных обстоятельств был лишен возможности работать на переднем уровне науки и потому пришлось заняться ее основами, фундаментом. Эти материалы в обсуждались или рассказывались Таргу, Седову, Ишлинскому, Раушенбаху, Легостаеву, Токарю, Алифанову, Журавлеву, Караску, Гребенникову, Сереброву, докладывалась на IV Съезде механиков в Киеве, в ГАИШе, МАИ, ИМ МГУ, а Краснодарском университете, на кафедре механики МФТИ и др. Обоснованность и необходимость создания неоптолемеевского языка для механики и прежде всего космонавтики, думается, не вызывает сомнений. Причем основы его чисто ньютоновские и не вызывают подозрений в некорректности. Хотя это не исключает возможности каких-то ошибок фактического, неконцептуального характера. Здесь открывается большой фронт работ с возможностью создания новых разделов механической науки, новых приложений ее, в том числе и для завоевания ведущих позиций в мировой науке российскими ученым, Сказано, что нет более практичного, чем хорошая теория. Заинтересовавшимся и желающим принять участие в разработке новой механики: телефон 8-926-314-9817, e-mail: vladimir@yur.ru, web: www.yur.ru Благодарю за внимание и терпение.