Презентация - Симметрия вокруг нас

Симметрия вокруг нас
Выполнил: ученик 11 «А» класса МБОУСОШ №54 г. Липецка Боровских Дмитрий Андреевич Руководитель: учитель по математике Цветкова Светлана Васильевна

Содержание:
Определение симметрии Виды симметрии: центральная симметрия (симметрия относительно точки) осевая симметрия (симметрия относительно прямой) зеркальная симметрия (симметрия относительно плоскости) симметрия вращения Симметрия вокруг нас: симметрия человеческого тела в природе в архитектуре в быту в физике в химии в литературе Заключение

Выдающийся математик Герман Вейль высоко оценил роль симметрии в современной науке.
"Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство". «Симметрия, обнаруживаемая и в жизни, и в искусстве, и в архитектуре, и в природе является одним из принципов гармоничного построения мира».
Толстой Л.Н. «Отрочество»
«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе.
Определение симметрии

В геометрии: Симметрия (означает «соразмерность» ) — свойство геометрической фигуры, расположенной в пространстве или на плоскости, заключающееся в закономерном повторении равных ее частей.
Определение симметрии
В биологии: Симметрия в биологии — это закономерное расположение подобных (одинаковых) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии.

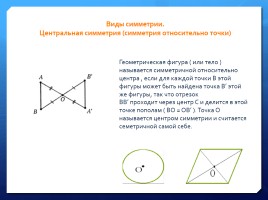
Виды симметрии. Центральная симметрия (симметрия относительно точки)
Геометрическая фигура ( или тело ) называется симметричной относительно центра , если для каждой точки B этой фигуры может быть найдена точка B’ этой же фигуры, так что отрезок BB’ проходит через центр C и делится в этой точке пополам ( BO = OB’ ). Точка O называется центром симметрии и считается семетричной самой себе.

Центральную симметрию имеют многие геометрические тела. К ним следует отнести все правильные многогранники (за исключением тетраэдра), все правильные призмы с четным числом боковых граней, некоторые тела вращения (эллипсоид, цилиндр, гиперболоид, тор, шар). Центр симметрии многогранников указывает на наличие двух равных и взаимно параллельных граней. Например, у параллелепипеда (рис.5.6) грань АА1'В1'В равна и параллельна грани В1В1А1А1. Рассмотрим симметричность вершин. Точке А симметричны две точки А1. Одна - относительно центра симметрии многогранника, другая - относительно центра симметрии грани. В свою очередь, точкам А1 симетрична точка А1' и т.д. Как видно из чертежа, грани параллелепипеда и прямо, и обратно параллельны. В случае октаэдра (рис.5.7) имеется только обратная параллельность граней, например, АВС и А1В1С1.

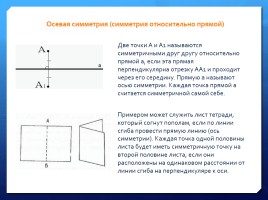
Осевая симметрия (симметрия относительно прямой)
Примером может служить лист тетради, который согнут пополам, если по линии сгиба провести прямую линию (ось симметрии). Каждая точка одной половины листа будет иметь симметричную точку на второй половине листа, если они расположены на одинаковом расстоянии от линии сгиба на перпендикуляре к оси.
Две точки A и A1 называются симметричными друг другу относительно прямой a, если эта прямая перпендикулярна отрезку AA1 и проходит через его середину. Прямую a называют осью симметрии. Каждая точка прямой a считается симметричной самой себе.

Прямоугольник ABCD имеет две оси симметрии: прямые m и l. Если чертеж перегнуть по прямой m или по прямой l, то обе части чертежа совпадут.
Квадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s. Если квадрат перегнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
Окружность с центром в точке О и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые: m, m1, m2, m3 ...

Зеркальная симметрия (симметрия относительно плоскости)
Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой фигуры может быть найдена точка E’ этой же фигуры, так что отрезок EE’ перпендикулярен плоскости S и делится этой плоскостью пополам ( EA = AE’ ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова (например, левая перчатка не подходит для правой руки и наоборот ). Они называются зеркально равными.

Предметы могут иметь одну, две, три и т.д. плоскостей симметрии. Например, прямая пирамида (рис.5.2а и 5.За), основанием которой является равнобедренный треугольник, симметрична относительно одной плоскости Р. Призма с таким же основанием (рис.5.2б и 5.3б) имеет две плоскости симметрии. У правильной шестиугольной призмы (рис.5.2в и 5.Зв) их семь. На рисунке не изображены те из них, которые подобно плоскостям Р и О, проходят через остальные диагонали и апофемы оснований. Тела вращения: шар, тор, цилиндр, конус и т.д. имеют бесконечное количество плоскостей симметрии.

Тело ( фигура ) обладает симметрией вращения, если при повороте на угол 360°/n ( здесь n – целое число ) вокруг некоторой прямой AB ( оси симметрии ) оно полностью совпадает со своим начальным положением. При n = 2 мы имеем осевую симметрию..
Симметрия вращения

Симметрия вокруг нас. Симметрия человеческого тела
Билатера́льная симме́трия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Этот тип симметрии характерен для большинства животных, включая человека. У билатерально-симметричного существа отличаются верхняя и нижняя, передняя и задняя части, и только правая и левая идентичны и являются зеркальным отображением друг друга.
Витрувианский человек Леонардо да Винчи, изображающий симметрию человека. Рисунок часто используется как неявный символ внутренней симметрии человеческого тела, и далее, Вселенной в целом.

В природе
На явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. Установлено, что в природе наиболее распространены два вида симметрии — "зеркальная" и "лучевая" ("радиальная”) (форма симметрии, при которой тело совпадает само с собой при вращении объекта вокруг определённой точки или прямой) симметрии.
"Зеркальной" симметрией обладает бабочка, листок или жук и часто такой вид симметрии называется "симметрией листка" или "билатеральной симметрией".
К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется "ромашко-грибной" симметрией.

Еще в 19-м веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел: "Все то, что растет или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой ("ромашко-грибной") симметрии. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии - "симметрии листка" (одна плоскость симметрии)".

Лёд — это уникальное вещество, способное образовывать более десяти различных кристаллических структур. снежинок.
Разгадка загадочной симметрии снежинок кроется в кристаллической решетке льда.
Практически весь лёд на планете кристаллизуется в гексагональной сингонии — его молекулы образуют правильные призмы с шестиугольным основанием. Именно шестиугольная форма решётки в конечном счёте обусловливает шестилучевую симметрию

В архитектуре
Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство зданий зеркально симметричны. Общие планы построек, фасады, орнаменты, карнизы, колонны обнаруживают соразмерность, гармонию.
Композиция здания очень важна. От нее в первую очередь зависит впечатление, которое производит архитектурное сооружение. Сочетание различных объемов — высоких и низких, прямолинейных и криволинейных, чередование пространств — открытых и закрытых — вот основные приемы, которыми пользуется зодчий, создавая архитектурные композиции.
Наиболее ясны и уравновешенны здания с симметричной композицией. Такие здания были характерны для архитектуры эпохи классицизма.

Но природа не терпит точных симметрий! Природа почти симметрична, но не абсолютно симметрична! Так, планетные орбиты, которые ещё Пифагором мыслились в виде совершенных окружностей, на самом деле оказались почти окружностями, но всё-таки не окружностями, а эллипсами. Нарушение симметрии обнаружено во многих явлениях ядерной физики. Помимо симметрии существует также понятие ассиметрии: Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. Примером удивительного сочетания симметрии и асимметрии является Покровский собор (храм Василия Блаженного) на Красной площади в Москве.

Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!

В быту
Орнамент — узор, основанный на повторе и чередовании составляющих его элементов. Предназначается для украшения различных предметов, архитектурных сооружений, произведений пластических искусств.

Бордюр — это узкая полоса обоев, предназначенная для декоративного оформления помещения.

В теоретической физике, поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения).
В физике
Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.

В химии
Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается на специфике физических и химических свойств молекул в изолированном состоянии, во внешнем поле и при взаимодействии с другими атомами и молекулами. Большинство простых молекул обладает элементами пространственной симметрии равновесной конфигурации: осями симметрии, плоскостями симметрии

В литературе
Палиндромами называют слова, предложения, стихи или иные произведения, которые читаются одинаково как с начала, так и с конца (имеют симметричный порядок букв)
ПРИМЕРЫ: А муза рада музе без ума да разума. A роза упала на лапу Азора. Вот сила типа капиталистов. Ешь немытого ты меньше! Кит на море романтик. Коту скоро сорок суток. Леша на полке клопа нашел. Мак чужд жучкам. Меня истина манит сияньем. Морда казака за кадром. Oколо Миши молоко. Он в аду давно. Ранил укусом осу кулинар. Тени нет. Я с леди все же свиделся.

Заключение

Симметрия — это не только математическое понятие. Его заимствовали из природы. А так как человек — это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Когда мы видим проявление симметрии в живой и неживой природе, то невольно испытываем чувство удовлетворения тем всеобщим, как нам кажется, порядком, который царит в природе. И даже при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.