Презентация - Механические волны
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 88%
- Слайдов: 19
- Просмотров: 1105
- Скачиваний: 86
- Размер: 1.68 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Механическая энергия. Закон сохранения энергии
Механическая энергия. Закон сохранения энергии Механическая работа. Мощность. КПД
Механическая работа. Мощность. КПД Урок обобщения знаний по теме «Механическое движение»
Урок обобщения знаний по теме «Механическое движение» Энергия топлива. Удельная теплота сгорания топлива. Закон сохранения и превращения энергии в механических и тепловых процессах
Энергия топлива. Удельная теплота сгорания топлива. Закон сохранения и превращения энергии в механических и тепловых процессах Механические колебания
Механические колебания Твёрдые тела. Механические свойства твёрдых тел (10 класс)
Твёрдые тела. Механические свойства твёрдых тел (10 класс) Кроссворд «Чудо - волны»
Кроссворд «Чудо - волны»
Слайды и текст этой онлайн презентации
Слайд 1

Механические волны
Слайд 2

Волна - это процесс распространения колебания в среде с течением времени
По физической природе различают
Механические волны упругие, звуковые, волны на поверхности жидкости
Электромагнитные волны свет, радиоволны, излучения
Слайд 3

Волна - это процесс распространения колебания в среде с течением времени
По ориентации возмущений различают
Поперечные волны -
Продольные волны -
Смещение частиц происходит вдоль направления распространения; могут распространяться только в упругих средах; необходимо наличие в среде силы упругости при сжатии; могут распространяться в любых средах. Примеры: звуковые волны
Смещение частиц происходит поперек направления распространения; могут распространяться только в упругих средах; необходимо наличие в среде силы упругости при сдвиге; могут распространяться только в твердых средах (и на границе двух сред). Примеры: упругие волны в струне, волны на воде
Слайд 4

Волна - это процесс распространения колебания в среде с течением времени
По характеру зависимости от времени различают
Упругие волны - механические возмещения (деформации), распространяющиеся в упругой среде. Упругая волна называется гармонической (синусоидальной), если соответствующие ей колебания среды являются гармоническими. Бегущие волны - волны, переносящие энергию в пространстве.
Слайд 5
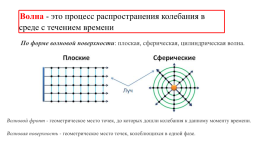
Волна - это процесс распространения колебания в среде с течением времени
По форме волновой поверхности: плоская, сферическая, цилиндрическая волна.
Волновой фронт - геометрическое место точек, до которых дошли колебания к данному моменту времени. Волновая поверхность - геометрическое место точек, колеблющихся в одной фазе.
Слайд 6
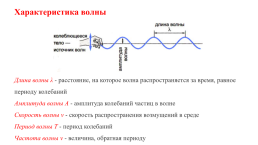
Характеристика волны
Длина волны λ - расстояние, на которое волна распространяется за время, равное периоду колебаний Амплитуда волны А - амплитуда колебаний частиц в волне Скорость волны v - скорость распространения возмущений в среде Период волны Т - период колебаний Частота волны ν - величина, обратная периоду
Длина волны λ - расстояние, на которое волна распространяется за время, равное периоду колебаний Амплитуда волны А - амплитуда колебаний частиц в волне Скорость волны v - скорость распространения возмущений в среде Период волны Т - период колебаний Частота волны ν - величина, обратная периоду
Слайд 7
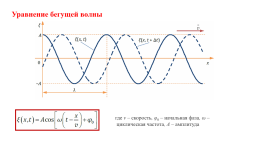
Уравнение бегущей волны
где v – скорость, φ0 – начальная фаза, ω – циклическая частота, A – амплитуда
где v – скорость, φ0 – начальная фаза, ω – циклическая частота, A – амплитуда
Слайд 8
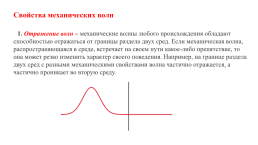
Свойства механических волн
1. Отражение волн – механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред. Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду.
1. Отражение волн – механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред. Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду.
Слайд 9

Свойства механических волн
2. Преломление волн – при распространении механических волн можно наблюдать и явление преломления: изменение направления распространения механических волн при переходе из одной среды в другую.
2. Преломление волн – при распространении механических волн можно наблюдать и явление преломления: изменение направления распространения механических волн при переходе из одной среды в другую.
Слайд 10

Свойства механических волн
3. Дифракция волн – отклонение волн от прямолинейного распространения, то есть огибание ими препятствий.
3. Дифракция волн – отклонение волн от прямолинейного распространения, то есть огибание ими препятствий.
Слайд 11

Свойства механических волн
4. Интерференция волн – сложение двух волн. В пространстве, где распространяются несколько волн, их интерференция приводит к возникновению областей с минимальным и максимальным значениями амплитуды колебаний
4. Интерференция волн – сложение двух волн. В пространстве, где распространяются несколько волн, их интерференция приводит к возникновению областей с минимальным и максимальным значениями амплитуды колебаний
Слайд 12

Интерференция и дифракция механических волн
Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. При наложении волн может наблюдаться явление интерференции. Явление интерференции возникает при наложении когерентных волн. Когерентными называют волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости. Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.
Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. При наложении волн может наблюдаться явление интерференции. Явление интерференции возникает при наложении когерентных волн. Когерентными называют волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости. Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.
Слайд 13

Интерференция и дифракция механических волн
Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания. Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же – в противоположных фазах, то наблюдается ослабление колебаний. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.
Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания. Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же – в противоположных фазах, то наблюдается ослабление колебаний. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.
Слайд 14
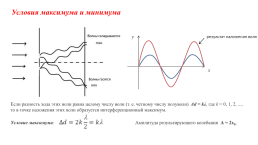
Условия максимума и минимума
Если разность хода этих волн равна целому числу волн (т. е. четному числу полуволн) Δd = kλ, где k = 0, 1, 2, ..., то в точке наложения этих волн образуется интерференционный максимум.
Условие максимума:
Амплитуда результирующего колебания А = 2x0.
Если разность хода этих волн равна целому числу волн (т. е. четному числу полуволн) Δd = kλ, где k = 0, 1, 2, ..., то в точке наложения этих волн образуется интерференционный максимум.
Условие максимума:
Амплитуда результирующего колебания А = 2x0.
Слайд 15
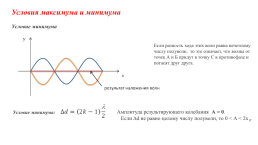
Условия максимума и минимума
Условие минимума
Если разность хода этих волн равна нечетному числу полуволн, то это означает, что волны от точек А и Б придут в точку С в противофазе и погасят друг друга.
Амплитуда результирующего колебания А = 0. Если Δd не равно целому числу полуволн, то 0 < А < 2х0.
Условие минимума:
Условие минимума
Если разность хода этих волн равна нечетному числу полуволн, то это означает, что волны от точек А и Б придут в точку С в противофазе и погасят друг друга.
Амплитуда результирующего колебания А = 0. Если Δd не равно целому числу полуволн, то 0 < А < 2х0.
Условие минимума:
Слайд 16

Дифракция волн
Явление отклонения от прямолинейного распространения и огибание волнами препятствий называется дифракцией. Соотношение между длиной волны (λ) и размерами препятствия (L) определяет поведение волны. Дифракция наиболее отчетливо проявляется, если длина набегающей волны больше размеров препятствия. Опыты показывают, что дифракция существует всегда, но становится заметной при условии d<<λ, где d – размер препятствия.
Явление отклонения от прямолинейного распространения и огибание волнами препятствий называется дифракцией. Соотношение между длиной волны (λ) и размерами препятствия (L) определяет поведение волны. Дифракция наиболее отчетливо проявляется, если длина набегающей волны больше размеров препятствия. Опыты показывают, что дифракция существует всегда, но становится заметной при условии d<<λ, где d – размер препятствия.
Слайд 17

Дифракция волн
Дифракция – общее свойство волн любой природы, которая происходит всегда, но условия её наблюдения разные. Волна на поверхности воды распространяется в сторону достаточно большого препятствия, за которым образуется тень, т.е. волнового процесса не наблюдается. Такое свойство используется при устройстве волноломов в портах. Если же размеры препятствия сравнимы с длиной волны, то за препятствием будет наблюдаться волнение. Позади него волна распространяется так, как будто препятствия не было вовсе, т.е. наблюдается дифракция волны.
Примеры проявления дифракции. Слышимость громкого разговора за углом дома, звуки в лесу, волны на поверхности воды.
Дифракция – общее свойство волн любой природы, которая происходит всегда, но условия её наблюдения разные. Волна на поверхности воды распространяется в сторону достаточно большого препятствия, за которым образуется тень, т.е. волнового процесса не наблюдается. Такое свойство используется при устройстве волноломов в портах. Если же размеры препятствия сравнимы с длиной волны, то за препятствием будет наблюдаться волнение. Позади него волна распространяется так, как будто препятствия не было вовсе, т.е. наблюдается дифракция волны.
Примеры проявления дифракции. Слышимость громкого разговора за углом дома, звуки в лесу, волны на поверхности воды.
Слайд 18

Стоячие волны
Стоячие волны образуются при сложении прямой и отраженной волны, если у них одинаковая частота и амплитуда. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Стоячие волны образуются при сложении прямой и отраженной волны, если у них одинаковая частота и амплитуда. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Слайд 19

Колебания струны
В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причем в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз.
Отсюда вытекает условие
Длинам волн соответствуют частоты
n = 1, 2, 3...Частоты vn называются собственными частотами струны.
Длинам волн соответствуют частоты
n = 1, 2, 3...Частоты vn называются собственными частотами струны.
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
