Презентация - Взаимное расположение прямой и окружности

Взаимное расположение прямой и окружности

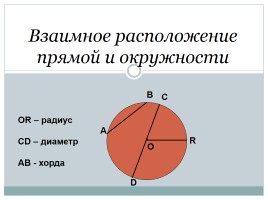
Взаимное расположение прямой и окружности
.
О
А
В
С
D
R
ОR – радиус СD – диаметр AB - хорда

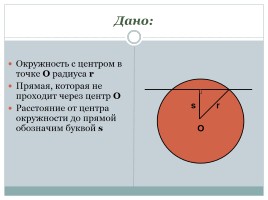
Дано:
Окружность с центром в точке О радиуса r Прямая, которая не проходит через центр О Расстояние от центра окружности до прямой обозначим буквой s
O
r
s

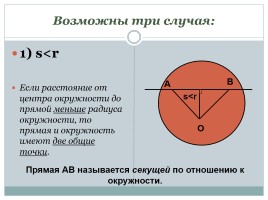
Возможны три случая:
1) sO
sА
В
Прямая АВ называется секущей по отношению к окружности.

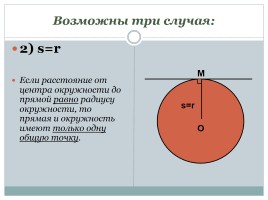
Возможны три случая:
2) s=r Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
O
s=r
M

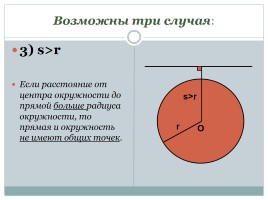
Возможны три случая:
3) s>r Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
O
s>r
r

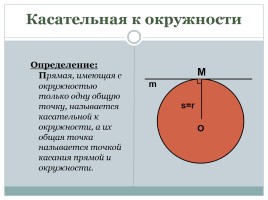
Касательная к окружности
Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
O
s=r
M
m

Выясните взаимное расположение прямой и окружности, если:
r = 15 см, s = 11см r = 6 см, s = 5,2 см r = 3,2 м, s = 4,7 м r = 7 см, s = 0,5 дм r = 4 см, s = 40 мм
прямая – секущая прямая – секущая общих точек нет прямая – секущая прямая - касательная

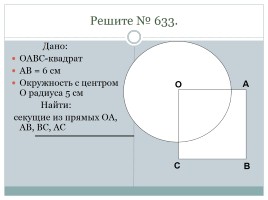
Решите № 633.
Дано: OABC-квадрат AB = 6 см Окружность с центром O радиуса 5 см Найти: секущие из прямых OA, AB, BC, АС
О
А
В
С
О

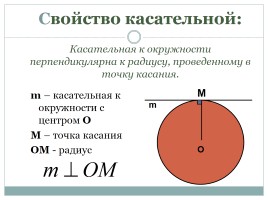
Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
m – касательная к окружности с центром О М – точка касания OM - радиус
O
M
m

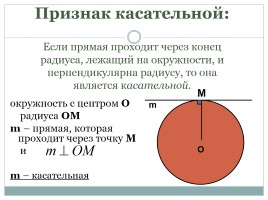
Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является касательной.
окружность с центром О радиуса OM m – прямая, которая проходит через точку М и m – касательная
O
M
m

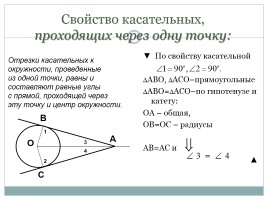
Свойство касательных, проходящих через одну точку:
▼ По свойству касательной ∆АВО, ∆АСО–прямоугольные ∆АВО=∆АСО–по гипотенузе и катету: ОА – общая, ОВ=ОС – радиусы АВ=АС и ▲
О
В
С
А
1
2
3 4
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.