Презентация - Задания к уроку «Квадрат суммы и квадрат разности»

Урок математики в 7 классе «Формулы сокращенного умножения» Квадрат суммы и квадрат разности

«Знание только тогда знание, когда оно приобретено усилиями своей мысли» Л.Н. Толстой

Игра «Третий лишний»
3² 9 6 4а² 16а² (4а)² (а + b)² (a+b)(a+b) a² + b² (c-d)(c+d) (c – d)² (c-d)(c-d) (7-3)² 16 40 (-a)² a² -a² (a-b)² (-a-b)² (a+b)²
=
=

1.Найдите квадраты выражений: а; -7; 2с; 5x²y³. 2.Найдите произведение выражений: p и q; 4x и 7y; a и 6b²c. 3.Чему равно удвоенное произведение этих выражений? 4.Прочитайте выражения: а) а+3; б) m-n; в) (х+у)²; г) (а- b)². 5.Упростить выражения: с · с; х² · х²; (a + b)(a + b). 6. Выполнить умножение: (x+3)(x+2); (а-5)(а+6).

Разделите следующие выражения на две группы и выполните действия: (х + у)2;   (x – y)2;    (p – s)2;  (p + s)2;  (a + b)2;  (a – b)2

1 группа (х + у)2 = (х + у)(х + у)=х2 + ху + ху + у2 = х2 + 2ху + у2 (p + s)2 = (p + s) (p + s)=p2 + ps + ps + s2 = p2 + 2ps + s2 (a + b)2 = (a + b)(a + b)=a2 + ab + ab + b2 = a2 + 2ab + b2 2 группа (x – y)2 = (х - у)(х - у)=x2 – xy – xy + y2 = x2 – 2xy + y2 (p – s)2 = (p - s) (p - s)=p2 – ps – ps + s2 = p2 – 2ps + s2 (a – b)2 = (a - b)(a - b)=a2 – ab – ab + b2 = a2 – 2ab + b2

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ квадрат суммы (а+b)² = а² +2аb+b² квадрат разности (а-b)² = а² -2аb+b²

(а+b)² = а² +2аb+b²
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого на второе выражение плюс квадрат второго выражения.

(а-b)² = а² -2аb+b²
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого на второе выражение плюс квадрат второго выражения.

(а+b)² = а² +2аb+b²
(а-b)² = а² -2аb+b²
Квадрат …. двух выражений равен квадрату первого выражения …. удвоенное произведение первого на второе выражение плюс квадрат второго выражения.
( ± )² = ² ± 2· + ²

Попробуйте раскрыть скобки, применяя новые правила
(d – s)2= (r + y)2= (m + f)2= (d – b)2=

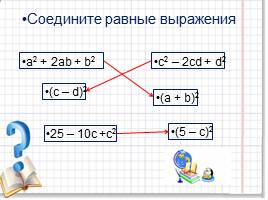
Соедините равные выражения
a2 + 2ab + b2
c2 – 2cd + d2
(c – d)2
(a + b)2
(5 – c)2
25 – 10c +с2

Заполни пропуски (поставь знак «+» или «-»):
1. (р – а)² = р² □2ра □а² 2. (8 – у)² = 64 □16у□у² 3. (s + z)² = s²□2sz□z² 4. (t + f)² = t² □2tf □f² 5. (d – m)(d – m) = d²□2dm□m²
(а+b)² = а² +2аb+b²
(а-b)² = а² -2аb+b²

Найдите и исправьте ошибки:
(2х + у)2 =  2х2 + 2ху + у2 (р – с)2 =  р2 – рс – с2 (3а – 4с)2 = 6а2 – 12ас – 4с2

I-ый уровень: Заполните пропуски, чтобы равенство оказалось верным. 1. (m - …) ² = m² - 20m +… ²= 2. 61² = 3600 + … + 1 =… = II-ой уровень: Представьте в виде алгебраической суммы. 3. (а + 2b)2= 4. (3m + 4c)2= III-ий уровень: Решите уравнение. 5. (4 - х)² - х(х - 5) = 4
Самостоятельная работа

I-ый уровень: Заполните пропуски, чтобы равенство оказалось верным. 1. (m - 10) ² = m² - 20m +10 ² 2. 61² = 3600 + 120 + 1 II-ой уровень: Представьте в виде алгебраической суммы. 3. (а + 2b)2=a2+4аb+4b2 4. (3m + 4c)2=9m2+24mc+16c2 III-ий уровень: Решите уравнение. 5. (4 - х)² - х(х - 5) = 4 16-8х+х²-х²+5х=4 -3х=-12 х=4
Самостоятельная работа (проверка)

Самостоятельная работа
(а + 2b)2= 2. (3m - 4c)2= 3. (5d + 3c)2= 4. (2r – 4x)2= 5. (3x + 2y)2=
a2+4аb+4b2
9m2-24mc+16c2
25d2+30dc+9c2
4r2-16rx+16x2
9x2+12xy+4y2

Выставление оценок:
Если вы набрали от 33 и более – оценка «5»; от 26 до 32 баллов – оценка «4»; от 19 до 25 баллов – оценка «3»; менее 19 баллов – «2»

Домашнее задание: выучить формулы, решить номера: на «3» достаточно выполнить № 28.1-28.3; на «4» решить № 28.4-28.6; на «5» решить № 28.7, 28.8, 28.12 Презентацию подготовила: учитель математики Пермякова Л.Д.