Слайды и текст этой онлайн презентации
Слайд 2
Основные понятия
Логика – это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.
Мышление всегда осуществляется через понятия, высказывания, умозаключения
Понятие – это форма мышления, которая выделяет существенные признаки предмета или классов предметов, позволяющие отличать их от других.
Высказывание – это формулировка своего понимания окружающего мира.
Высказывание может быть истинно или ложно
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.
Слайд 3
Логические выражения и операции
Алгебра логики или алгебра высказываний –это операции над высказываниями.
Логическая переменная –это простое высказывание содержащее только одну мысль. Ее значениями могут быть только ИСТИНА и ЛОЖЬ (1 и 0)
Логическая функция – составное высказывание.
Логические операции – логическое действие
Слайд 4
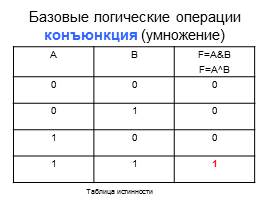
Базовые логические операции конъюнкция (умножение)
А В F=A&B
F=A^B
0 0 0
0 1 0
1 0 0
1 1 1
Таблица истинности
Слайд 5
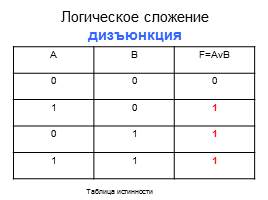
Логическое сложение дизъюнкция
А В F=AvB
0 0 0
1 0 1
0 1 1
1 1 1
Таблица истинности
Слайд 6
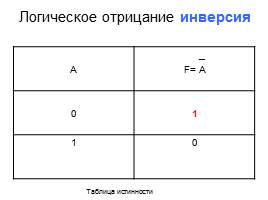
Логическое отрицание инверсия
А _
F= A
0
1
1 0
Таблица истинности
Слайд 7
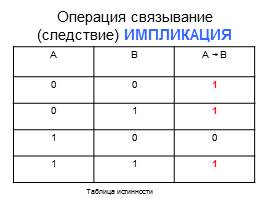
Операция связывание (следствие) ИМПЛИКАЦИЯ
A
B A B
0 0 1
0 1 1
1 0 0
1 1 1
Таблица истинности
Слайд 8
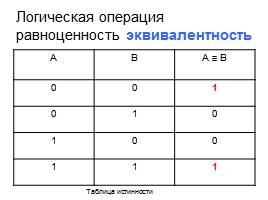
Логическая операция равноценность эквивалентность
A B A B
0 0 1
0 1 0
1 0 0
1 1 1
Таблица истинности
Слайд 9
Логические законы и правила преобразования логических выражений
Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них переменных.
Закон двойного отрицания:
=
А = А
Двойное отрицание исключает
отрицание
Слайд 10
Закон тождества
А = А
Закон непротиворечия
А & A = 0
Закон исключение третьего
A v A = 1
Слайд 11
Закон общей инверсии (Закон де Моргана)
Для логического сложения:
A v B = A & B
Для логического умножения:
A & B = A v B
Слайд 12
Переместительный
( коммутативный) закон
Для логического сложения:
А v B = B v A
Для логического умножения:
A & B = B & A
Результат выполнения операции не зависит от того, в каком порядке берутся эти высказывания
Слайд 13
Сочетательный (ассоциативный) закон
Для логического сложения:
(A v B) v C = A v (B v C)
Для логического умножения:
(A & B) & C = A & (B & C)
При одинаковых знаках скобки можно ставить произвольно или вообще опускать
Слайд 14
Распределительный (дистрибутивный) закон
Для логического сложения:
(A v B) & C = (A & C) v (B & C)
Для логического умножения:
(A & B) v C = (A v C) & (B v C)
Определяет правила выноса общего высказывания за скобку
Слайд 15
Для составления таблицы истинности N количества переменных необходимо определить: сколько строк в этой таблице будет.
Для этого используют формулу:
Количество строк = 2n
Слайд 16
Практические задания.
Определить истинность составного высказывания (A & B) & (C v D), состоящее из простых высказываний:
А – (принтер- устройство ввода информации);
В – (процессор – устройство хранения информации);
С – (монитор – устройство вывода информации);
D – ( клавиатура – устройство обработки информации)
Слайд 17
Найти значения логических выражений
F= (0 v 0) v (1 v 1)
F= (1 v 1) v (0 v 1)
F= (0 & 0) & (1 & 1)
F= (1 & 1) & (0 & 1)
F= (0 & 1) & 1
F= 1 & (1 & 1) & 1
Слайд 18
((1 v 0) & (1 & (0 v 1)) & (0 v 1)
((1 v 0) & (1 v 0)) & (0 v 1)
((1 & 0) v (1 & 0)) v 1
((1&0)v0)&(0v1)
((0 & 0) & 0) & (1 v 1)
Слайд 19
Построить таблицу истинности для выражения
F = (A v B) & (- A v -B)
F = X v Y & - Z
Слайд 20
Записать в виде логических выражений
Z является min (Z,Y)
A является max (A,B,C)
Любое из чисел X,Y,Z положительно
Любое из чисел X,Y,Z отрицательно
Хотя бы одно из чисел K,L,M не отрицательно
Хотя бы одно из чисел X,Y,Z не меньше 12
Все числа X,Y,Z равны 12
Если X делится на 9, то X делится на 3
Если Х делится на 2, то Х четное число
Слайд 21
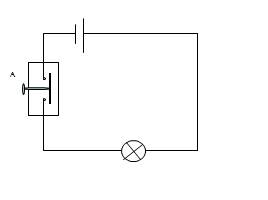
Логические основы устройства компьютера
Логические элементы компьютера оперируют с сигналами, представляющие собой электрические импульсы.
Есть импульс – 1;
Нет импульса – 0.
Слайд 23
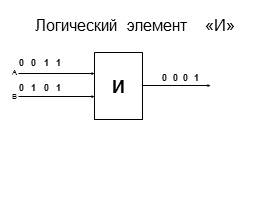
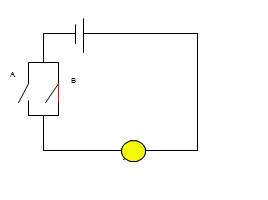
Логический элемент «И»
И
А
В
0
0
0
0
1
1
1
0
1
0
0
1
Слайд 26
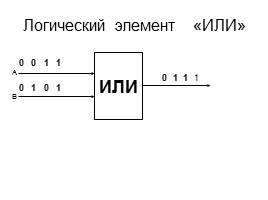
Логический элемент «ИЛИ»
ИЛИ
А
В
0
0
0
0
1
1
1
0
1
1
1
1
Слайд 29
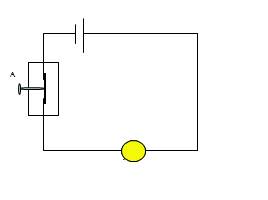
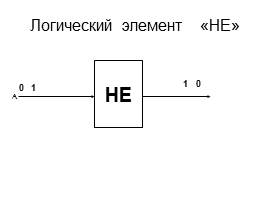
Логический элемент «НЕ»
НЕ
А
0
1
0
1
Слайд 30
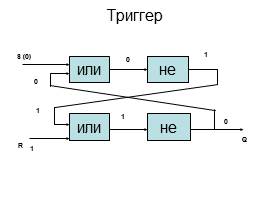
Триггер
или
не
или
не
не
S (0)
0
1
1
0
Q
R
1
0
1
Слайд 31
Триггер
или
не
или
не
не
S (1)
1
0
0
1
1
Q
R
0
Слайд 32
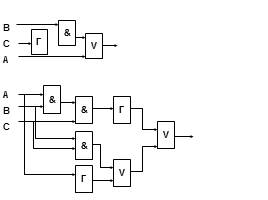
Построить логическую схему по выражению и вычислить его значение:
F = X v Y & X, при X = истина, Y= ложь
F = X & Y v Г (Y v X), при Х=1, Y=0
А = Г (A V B & C), при А=1, В=1, С=1
F = Г A V B & C, ПРИ А=0, В=1, С=1
F = (A V B) & (C v B), при А=1, В=0, С=1
F = Г (А & B & C), при А=1, В=1, С=0
F= Г (A & B & C) v В & A, при А=0, В=0
Слайд 33
&
Г
V
В
С
А
&
&
&
Г
Г
V
V
А
В
С
Слайд 34
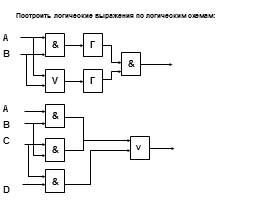
Построить логические выражения по логическим схемам:
&
V
Г
Г
&
А
В
&
&
&
V
A
B
C
D
Слайд 35
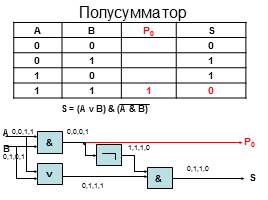
Полусумматор
А В P0 S
0 0 0
0 1 1
1 0 1
1 1 1 0
S = (A v B) & (A & B)
&
v
&
A
B
S
0,0,1,1
0,0,0,1
1,1,1,0
0,1,1,0
0,1,1,1
0,1,0,1
P0
Слайд 36
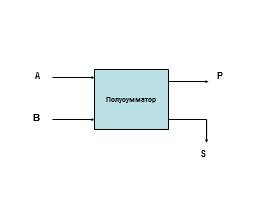
Полусумматор
A
B
B
P
S
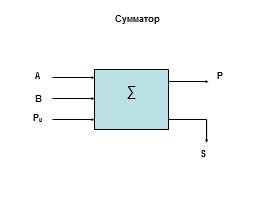
Слайд 38
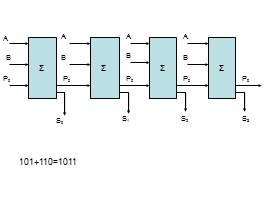
∑
∑
∑
∑
A
B
A
A
A
B
B
B
P0
P0
P0
P0
P0
S3
S2
S1
S0
101+110=1011
Слайд 39
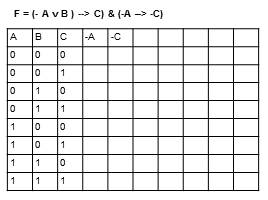
A B C -A -C
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
F = (- A v B ) --> C) & (-A –> -C)
 Основы логики: логические величины и формулы
Основы логики: логические величины и формулы Логико-психологические основы использования компьютера в процессе формирования учебной деятельности
Логико-психологические основы использования компьютера в процессе формирования учебной деятельности Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Логика. Математические основы информатики.
Логика. Математические основы информатики. Иллюстративная презентация по трем основным линиям романа «Мастер и Маргарита» 1928-1940 гг.
Иллюстративная презентация по трем основным линиям романа «Мастер и Маргарита» 1928-1940 гг. Основание Воронежа
Основание Воронежа Юрта-основное жилище кочевых Татар и Башкир
Юрта-основное жилище кочевых Татар и Башкир