Презентация - Применение теорем синусов и косинусов

Школа-гимназия № 95 Учитель математики: Отрощенко Елена Михайловна
Тема: Применение теорем синусов и косинусов.

Эпиграф к уроку: «Знания по геометрии или умение пользоваться формулами необходимы почти каждому мастеру.» А.Н. Колмогоров. Цель урока: показать связь теории с практикой, способствовать совершенствованию навыков решения практических задач, применяя теоремы синусов и косинусов. Задачи:1. повторение: теоремы синусов, теоремы косинусов и умение использовать их при решении задач, применять соотношения между сторонами и углами треугольника в решении задач стандартного уровня с переходом на более высокий уровень; 2. показать связь теории с практикой при помощи решения различных задач, способствовать совершенствованию навыков решения практических задач.

Фронтальный опрос. Что называют решением треугольников? Какие теоремы применяются при решении треугольников? Сформулируйте теорему синусов? Сформулируйте следствие из теоремы синусов? Сформулируйте теорему косинусов? Какая связь между сторонами и углами в треугольнике? Какие задачи при этом можно выделить? (по стороне и двум прилежащим к ней углам; по двум сторонам и углу между ними; по трём сторонам; по стороне, прилежащему к ней углу и стороне противолежащей данному углу) . Каким может быть ? Ответ: =300 или =1500. Как можно вычислить вид треугольника? (с помощью т. Пифагора и т.синусов и т. косинусов) Можно ли построить треугольник с любыми сторонами?

III. Самостоятельная работа по карточкам: (карточка №1) Взаимопроверка.

IV. Индивидуальное задание. (карточка №2)

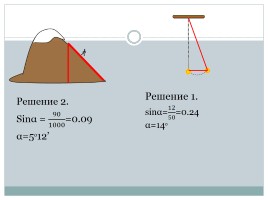
Решение 2. Sinα = 90 1000 =0.09 α=5ᵒ12’
Решение 1. sinα= 12 50 =0.24 α=14ᵒ

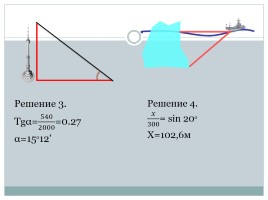
Решение 3. Tgα= 540 2000 =0.27 α=15ᵒ12’
Решение 4. ???? 300 = sin 20ᵒ X=102,6м

V. Работа индивидуальная, с обсуждением в группах.

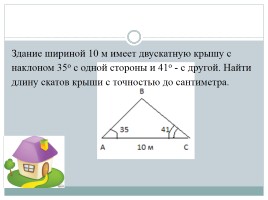
Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o - с другой. Найти длину скатов крыши с точностью до сантиметра.

В 12ч00мин нарушитель свернул с основной магистрали и помчался по шоссе со скоростью 140 км/ч. В 12ч00мин инспектор ГАИ помчался по просёлку со скоростью 70 км/ч на перерез нарушителю. Успеет ли инспектор остановить нарушителя у перекрёстка шоссе и просёлка?

Рефлексия.
Запишите ключевые слова урока (новые термины)  
Что было легко?      
Что было трудно?      
Твое продвижение по теме:  

Спасибо за внимание!