Презентация - Измерение скорости полёта пули

Министерство общего и профессионального образования Свердловской области Муниципальное автономное общеобразовательное учреждение «Верхнедубровская средняя общеобразовательная школа»
Измерение скорости полёта пули
Исполнитель:
Лукинских Татьяна
ученица 10 класса
Руководитель:
Купреева С.А., учитель физики, первой кв.категории
Верхнее Дуброво 2015

Актуальность

Первоначально я предположила, что в нашем мире существует какой-нибудь физический способ для определения скорости полета пули и его можно осуществить на практике.

Задачи Методы
1.Найти нужную информацию 1.Аналитический метод решения задачи по механике
2. Проанализировать полученную информацию и ресурсы 2.Экспериментальный метод решения задачи
3. Выполнить запланированные технологические задачи 3.Экспериментальная проверка эталоном (промышленным прибором)
4. Проанализировать выполненный проект

Параболический метод
Криволинейное баллистическое движение тела можно рассматривать как результат сложения двух прямолинейных движений: равномерного движения по горизонтали и равнопеременного движения по вертикали под действием силы тяжести.
х

Эксперимент
Расстояние от ружья до цели – S=386 cм. Смещение по вертикали Х от места попадания пули до выбранной цели оказалось 3мм или 0,003м. Тогда время падения пули t =√(2x/g) = √((2*0,003)/9,8)=0,025c. Тогда скорость пули можно определить: V= S/t=(3,86 м )/(0,025 с ) = 154,4 м/с

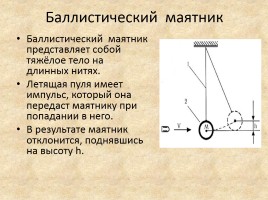
Баллистический маятник
Баллистический маятник представляет собой тяжёлое тело на длинных нитях. Летящая пуля имеет импульс, который она передаст маятнику при попадании в него. В результате маятник отклонится, поднявшись на высоту h.

Баллистический Маятник
Закон сохранения импульса: m1*V=(M+m1)U , где m1V- импульс пули, (M+m1)U- импульс маятника после выстрела. Закон сохранения энергии Ек=Ер ((M+m1 )*U^2)/2 = (M+m1)hg U2/2=hg

Баллистический Маятник
Длина подвеса 200 см от оси подвеса до середины бруска m10 пуль=6,88 г m1 пули=0,688 г Расстояние до маятника=1,5 м Отклонение маятника 14 см Mмаятника=200,38 г M в эксперименте=Mмаятника+m1пули =201,068г

Баллистический Маятник
По теореме Пифагора: ОА= √(22-x2 )=√(4-0,142)=√3,98 =1,99 м Тогда высота подъема маятника: h=2м-ОА=2-1,99 =0,01м=1см Скорость маятника: U=√2gh=√(2*9,8*0,01)=√0,0298 = 17 м/с Скорость пули: V=((M+m1)*U)/m1 = ((201,068+0,688)*0,17)/0,688 = 49,9 м/с
А
О
В

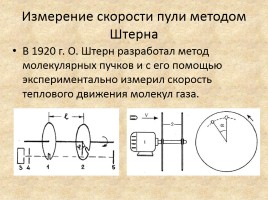
Измерение скорости пули методом Штерна
В 1920 г. О. Штерн разработал метод молекулярных пучков и с его помощью экспериментально измерил скорость теплового движения молекул газа.

Измерение скорости пули методом Штерна
В качестве конструкции механической установки Штерна используем два диска, закрепленных на одной вращающейся оси проигрывателя пластинок.

Опыт по методу Штерна
Расстояние между дисками h=10,5 см=0,105 м. Радиус картонных дисков составил: R=10 см=0,1 м. Проигрыватель произвел 5 оборотов за 8,27 с Отсюда время одного оборота Т=1,654 с.

Опыт по методу Штерна
Отклонение L = 3 мм =0,003 м Применяем формулу длины окружности – 2πR = 2*3,14*0,1. Для определения времени Х пролета пули воспользуемся пропорцией: Т /х = 2πR/L 1,654/х = ( 2*3,14*0,1)/0,003, Отсюда время полета пули между двумя дисками х=(1,654*0,003)/(2*3,14*0,1)=0,008 с.

Опыт по методу Штерна
Теперь найдём скорость пули : V=S/t V=(0,105 м)/(0,008 с)=13,125 м/с Погрешность этого эксперимента составляет: V/(Vст.)*100= 13,125/144*100=9%

Хронограф - прибор для измерения скорости пули.
Электронное устройство, которое имеет максимально малую погрешность. Любой способ непосредственного измерения величины имеет малую погрешность. Кроме того прибор позволяет определить непосредственно скорость пули при выстреле – начальную скорость пули.

Хронограф
1 выстрел=142 м/с 2 выстрел=144 м/с 3 выстрел=144 м/с 142+144+144=430 м/с – сумма значений скорости пули трех выстрелов (430 м/с)/3 =143.3м/с – среднее значение.

Анализ экспериментов.
№ эксперимента. Результат эксперимента
1 эксперимент. Параболический метод. 154,4 м/с
2 эксперимент. Баллистический маятник. 49,9 м/с
3 эксперимент. Метод Штерна. 13,125 м/с
4 эксперимент. Хронограф. 143,4 м/с

Заключение
В начале проекта я выдвинула гипотезу о том, что существует физический способ определения скорости полета пули. Моя гипотеза подтвердилась. Действительно, есть такие способы и при том не один.
Школьная физика далека от реальности!

Спасибо за внимание!!!