Презентация - Степень

Алгебра 11 класс, УМК Мордковича А.Г.
Степень
Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной

Из истории
Понятие степени с натуральным показателем сформировалось ещё у древних народов. Квадрат и куб числа использовались для вычисления площадей и объемов. Степени некоторых чисел использовались при решении отдельных задач учеными Древнего Египта и Вавилона.

Из истории
В III веке вышла книга греческого ученого Диофанта “Арифметика”, в которой было положено начало введению буквенной символики. Диофант вводит символы для первых шести степеней неизвестного и обратных им величин. В этой книге квадрат обозначается знаком k с индексом r; куб – знаком k c индексом r и т.д.

Из истории
Все началось с Древнегреческого ученого Пифагора. У него была целая школа, и всех его учеников называли пифагорейцами. Они придумали, что каждое число можно представить в виде фигур. Например, числа 4, 9 и 16 они представляли в виде квадратов.

Из истории
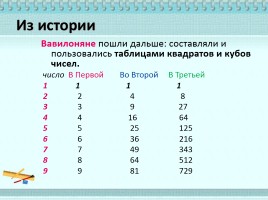
Вавилоняне пошли дальше: составляли и пользовались таблицами квадратов и кубов чисел. число В Первой Во Второй В Третьей 1 1 1 1 2 2 4 8 3 3 9 27 4 4 16 64 5 5 25 125 6 6 36 216 7 7 49 343 8 8 64 512 9 9 81 729

Из истории
Индийские ученые независимо от всех остальных открыли и оперировали степенями с натуральными показателями до 9 включительно, называя их с помощью комбинации трех слов: “ва” (2-я степень, от слова “варга” – квадрат), “гха” (3-я степень, от “гхана” - куб) и “гхата” (слово указывающее на сложение показателей). Например: 4 степень – “ва-ва”, 5-ая – “ва-гха-гхата”, 6-ая – “ва-гха”.

Из истории
XVI век. В этом веке понятие степени расширилось: его стали относить не только к конкретному числу, но и к переменной. Как тогда говорили «к числам вообще» Английский математик Симон Стевин придумал запись для обозначения степени: запись 3(3)+5(2)–4 обозначала такую современную запись 33 + 52 – 4.

Из истории
Дробные показатели степени и наиболее простые правила действии над степенями с дробными показателями встречаются у французского математика Николая Орема (1323–1382 гг.) в его труде “Алгоризм пропорций”.

Из истории
Равенство, а⁰ = 1 для а ≠ 0 применял в своих трудах в начале ХV века самаркандский ученый Гиясаддин Каши Джемшид.

Из истории
Независимо от него нулевой показатель был введен Николаем Шюке в ХV веке. Известно, что Николай Шюке (1445–1500 гг.), рассматривал степени с отрицательными и нулевым показателями.

Из истории
Позже дробные и отрицательные, показатели встречаются в “Полной арифметике” (1544 г.) немецкого математика Михеля Штифеля и у Симона Стевина. С.Стевин предположил подразумевать под а⅟ ⁿ корень.

Из истории
Современные определения и обозначения степени с нулевым, отрицательным и дробным показателем берут начало от работ английских математиков Джона Валлиса (1616–1703) и Исаака Ньютона (1643–1727).

Знаем
Мы умеем вычислять значение степени аⁿ с любым целочисленным показателем n, руководствуясь следующими определениями: 1) если n = 1, то а¹ = а; 2) если n = 0 и а ≠ 0 , то а⁰ = 1; 3) если n = 2;3;4;5;… , то аⁿ=а·а·а·…·а (n раз) 4) если n =1;2;3;4;5;… , и а ≠ 0 , то а⁻ⁿ=1/аⁿ

Знаем
Свойства: Пусть а>0 и в>0; k и m – целые числа, тогда:

Определение
Степенью числа а>0 с рациональным показателем r = m/n, где m-целое число, а n-натуральное число (n>1), называется число Итак, по определению При а<0 рациональная степень числа а не определяется!!!

Оказывается
Если основания степеней положительны, то известные нам свойства выполняются для любых показателей степени.

Найти значение выражения
1) 2)

Решаем
Найти значение выражения Решение: Самостоятельно:
Ответ: 10

Решить в парах
1) 2)
Ответы: 3/8 27√2

Решить самостоятельно
1) 2)
Ответ: 4/5 128/27

Источники
http://aida.ucoz.ru – фон слайда С.Стевина http://img1.liveinternet.ru/images/attach/c/1/57/984/57984922_Stifel_Michel.jpg Диофант http://www.tovima.gr/files/1/2014/02/28/0_diofant.jpg Пифагор http://www.bdn-steiner.ru/modules/Coppermine/albums/Deyateli/af_08_pifagor.jpg М.Штифеля http://www.mccme.ru/istolimp/2006/opim_htm/opim2_vstuplenie._files/image003.gif Д.Валлиса http://www.illc.uva.nl/Wallis/uploaded_files/1wallis.gif И.Ньютона http://www.24sata.hr/image/nastali-iz-hobija-slavnih-a-danas-su-dio-svakodnevice-900x600-20070624-20101019004049-14514.jpg Н.Орема http://afishalviv.net/php_uploads/images/eventimages/ArticlePortletImage_10435.jpg Н. Шюке http://images.cdn.bridgemanart.com/api/1.0/image/600wm.EUL.7066520.7055475/253428.jpg Г. Каши http://www.gencgelisim.com/v2/images/stories/omer-hayyam-kimdir.jpg Задания взяты: Задачник А.Г.Мордковича «Алгебра и начала анализа» 10-11 класс,- М., Мнемозина,2012 А.Н. Колмогоров и др. «Алгебра и начала анализа» Учеб. для 10-11 классов сред. шк.,- М., Просвещение,1990
http://www.flconf.org/education/wp-content/uploads/2011/04/5107103-1886x2550-1-1024x757.jpg