Презентация - Геометрическое место точек презентация к уроку

Геометрическое место точек презентация к уроку
Выполнила учитель математики Соболева Л.И. МБОУ СОШ №35

Основные сведения о ГМТ
Геометрическое место точек (сокращенно ГМТ), обладающих некоторым свойством, - это фигура, состоящая из всех точек, для которых выполнено это свойство. Решение задачи на поиск ГМТ должно содержать доказательство того что: Точки обладающие требуемым свойством, принадлежат фигуре Ф, являющейся ответом задачи; Все точки фигуры Ф обладают этим свойством. ГМТ , обладающих двумя свойствами является пересечением(т.е. общей частью) двух фигур: ГМТ обладающих первым свойством , и ГМТ обладающих вторым свойством.

Три важнейших ГМТ
ГМТ , равноудаленных от точек А и В, является серединным перпендикуляром к отрезку АВ; ГМТ, удаленных на расстояние R от данной точки O, является окружностью радиуса R с центром О; ГМТ, из которых данный отрезок АВ виден под данным углом, является объединением двух дуг окружностей, симметричных относительно прямой АВ (точки А и В не принадлежат ГМТ).

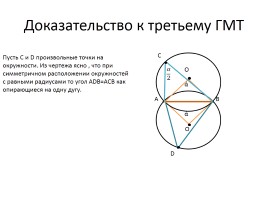
Доказательство к третьему ГМТ

Пусть С и D произвольные точки на окружности. Из чертежа ясно , что при симметричном расположении окружностей с равными радиусами то угол ADB=ACB как опирающиеся на одну дугу.

Задача на ГМТ №1
A
B
O
M
X
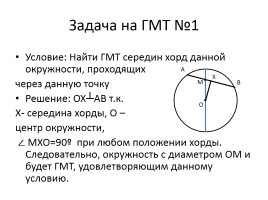
Условие: Найти ГМТ середин хорд данной окружности, проходящих через данную точку Решение: OX┴AB т.к. X- середина хорды, О – центр окружности, ∠ MXO=90º при любом положении хорды. Следовательно, окружность с диаметром ОМ и будет ГМТ, удовлетворяющим данному условию.

Задача на ГМТ №2
 
B(a,0)

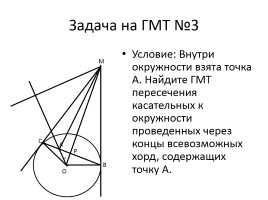
Задача на ГМТ №3
Условие: Внутри окружности взята точка А. Найдите ГМТ пересечения касательных к окружности проведенных через концы всевозможных хорд, содержащих точку А.
 

Решение задачи №3
 

Заключение
Задачи на ГМТ нечасто встречаются в школьной программе , но решение их развивает математический кругозор.