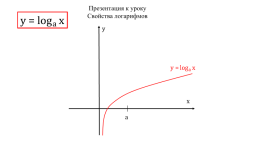
Презентация - Логарифмы и их свойства

Л О Г А Р И Ф М Ы И И Х С В О Й С Т В А .
Возведение в степень имеет два обратных действия. Если
а х = b,
то отыскание a есть одно обратное действие – извлечение корня; нахождение же b – другое,
л о г а р и ф м и р о в а н и е.
Для чего были придуманы логарифмы ?
Конечно, для ускорения и упрощения вычислений.
(1)
1

Изобретатель первых логарифмических таблиц, Непер, так говорил о своих побуждениях:
«Я старался, насколько мог и умел, отделаться от трудности и скуки вычислений, докучность которых обычно отпугивает весьма многих от изучения математики».
Современник Непера, Бригг, прославившийся позднее изобретением десятичных логарифмов, писал, получив сочинение Непера:
«Своими новыми и удивительными логарифмами Непер заставил меня усиленно работать и головой и руками. Я надеюсь увидеть его летом, так как никогда не читал книги, которая нравилась бы мне больше и приводила бы в большее изумление».
2

Бригг осуществил свое намерение и направился в Шотландию, чтобы посетить изобретателя логарифмов. При встрече Бригг сказал:
«Милорд, я предпринял это долгое путешествие только для того, чтобы видеть Вашу особу и узнать, с помощью какого инструмента разума и изобретательности Вы пришли впервые к мысли об этом превосходном пособии для астрономов, а именно – логарифмах; но, милорд, после того, как Вы нашли их, я удивляюсь, почему никто не нашел их раньше, настолько легкими они кажутся после того, как о них узнаёшь».
Великий математик говорил об астрономах, так как им приходится делать особенно сложные и утомительные вычисления. Но слова его с полным правом могут быть отнесены ко всем вообще, кому приходится иметь дело с числовыми выкладками.
3

О П Р Е Д Е Л Е Н И Е.
Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить b (где а> 0, а≠1).
Вспомните уравнение из первого слайда: а х = b Мы оговорили, что нахождение b – логарифмирование. Математики договорились записывать это так:
Log a b = x
(читается: «логарифм b по основанию a»).
Например, log 5 25 = 2, так как 5 2 = 25.
Log 4 (1/16) = - 2, так как 4 -2 = 1/16.
Log 1/3 27 = - 3, так как (1/3) – 3 = 27.
Log 81 9 = ½, так как 81 ½ = 9.
4

Log 2 16; log 2 64; log 2 2; Log 2 1 ; log 2 (1/2); log 2 (1/8); Log 3 27; log 3 81; log 3 3; Log 3 1; log 3 (1/9); log 3 (1/3); Log1/2 1/32; log1/2 4; log0,5 0,125; Log0/5 (1/2); log0,5 1; log1/2 2.
Вычислить:
5

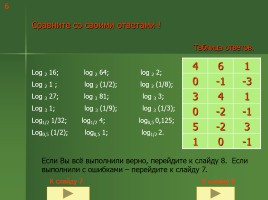
Сравните со своими ответами !
Log 2 16; log 2 64; log 2 2; Log 2 1 ; log 2 (1/2); log 2 (1/8); Log 3 27; log 3 81; log 3 3; Log 3 1; log 3 (1/9); log 3 (1/3); Log1/2 1/32; log1/2 4; log0,5 0,125; Log0,5 (1/2); log0,5 1; log1/2 2.
Таблица ответов.
4 6 1
0 -1 -3
3 4 1
0 -2 -1
5 -2 3
1 0 -1
Если Вы всё выполнили верно, перейдите к слайду 8. Если выполнили с ошибками – перейдите к слайду 7.
6

7
Правильное решение примеров 1 столбца:
Log 2 16 = 4, так как 2 4 = 16. Log 2 1 = 0, так как 2 0 = 1. Log 3 27 = 3, так как 3 3 = 27. Log ½ 1/32 = 5, так как (1/2) 5 = 1/32. Log 0,5 (1/2) = 1, так как (0,5) 1 = (1/2)1 = ½.
Проверьте 2 и 3 столбец, исправьте ошибки самостоятельно. Если появились вопросы – обратитесь к учителю.

Определение логарифма можно записать так:
a log a b = b
Это равенство справедливо при b>0, а>0, а≠1. Его обычно называют основным логарифмическим тождеством.
Например: 2 log 2 6 = 6; 3 – 2 log3 5 = (3 log 3 5 ) – 2 = 5 – 2 = 1/25.
Вычислите:
3 log 3 18; 3 5log 3 2; 5 log 5 16; 0,3 2log 0,3 6; 10 log 10 2; (1/4) log(1/4) 6; 8 log 2 5; 9 log 3 12.
8

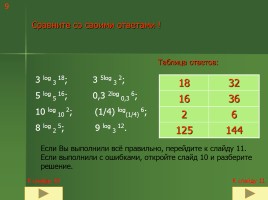
Таблица ответов:
18 32
16 36
2 6
125 144
Если Вы выполнили всё правильно, перейдите к слайду 11. Если выполнили с ошибками, откройте слайд 10 и разберите решение.
Сравните со своими ответами !
3 log 3 18; 3 5log 3 2; 5 log 5 16; 0,3 2log 0,3 6; 10 log 10 2; (1/4) log(1/4) 6; 8 log 2 5; 9 log 3 12.
9

10
Правильное выполнение некоторых заданий.
Остальные задания проверьте ещё раз самостоятельно. Если появился вопрос – обратитесь к учителю.

С В О Й С Т В А Л О Г А Р И Ф М О В .
ОСНОВНЫЕ СООТНОШЕНИЯ ДОПОЛНИТЕЛЬНЫЕ СООТНОШЕНИЯ
Логарифм произведения: Log c (ab) = log ca + log c b. Логарифм частного: Log c (a/b) = log c a – log c b. Логарифм степени: Log c a k = k log c a. Переход к новому основанию: Log b a = log c a / log c b. Log a b = 1/ log b a, Log a m b n = n/m (log a b).
Log a 1 = 0; log a a = 1; log a (1/a) = - 1; log a a m = m; Log a m a = 1/m.
11

Приведем примеры применения формул: Log 6 18 + log 6 2 = log 6 (18·2) = log 6 36 = 2 Log 12 48 – log 12 4 = log 12 (48/4) = log 12 12 = 1
А здесь выполните вычисления самостоятельно:
Log 10 5 + log 10 2; Log 12 2 + log 12 72; Log 2 15 – log 2 (15/16); Log1/3 54 – log1/3 2; Log 5 75 – log 5 3; Log 8 (1/16) – log 8 32; Log 8 12 – log 8 15 + log 8 20; Log 9 15 + log 9 18 – log 9 10;
12

13
Примеры выполнения некоторых заданий…
Log 10 5 + log 10 2 = log 10 (5 . 2) = log 10 10 = 1 Log 1/3 54 – log 1/3 2 = log 1/3 (54/2) = log 1/3 27 = -3 Log 8 12 – log 8 15 + log 8 20 = log 8(12/15) + log 8 20 = = log 8 (4/5 . 20) = log 8 16 = 2
Остальные задания проверьте самостоятельно. Если появился вопрос, обратитесь к учителю.
1
2
4
-3
2
-3
4/3
3/2
И таблица ответов:

14
* Вычислите :
После выполнения этого задания обратитесь к учителю.

Домашнее задание.
15
Если со всеми предложенными заданиями Вы справились без ошибок, то Ваше домашнее задание: п.37, № 489, № 490, № № 495(b,в), №496(b,в,г).
Если при выполнении предложенных заданий Вы испытывали затруднения и не смогли всё выполнить правильно, то Ваше домашнее задание: п.37, № 476, № 483(b,в), № 488, № 495(b,в).

« СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ УСВОИЛ НИЧЕГО НОВОГО И НИЧЕГО НЕ ПРИБАВИЛ К СВОЕМУ ОБРАЗОВАНИЮ.»
16
Я. А. КОМЕНСКИЙ.

17
СПАСИБО ЗА УРОК!
Prezentacii.com