Презентация - Механические колебания

Механические колебания
Виды колебаний.

Колебания бывают свободными и вынужденными
Свободные колебания происходят без воздействия внешних периодически изменяющихся сил.     При наличии таких сил колебания называют вынужденными. Тряска автомобиля, движущегося по неровной дороге, движение качелей, которые периодически подталкивают, - все это вынужденные колебания. На рисунке показан пример вынужденных колебаний, которые вызваны оборотами ручки. Частота и период вынужденных колебаний совпадают с частотой и периодом изменений внешней силы. Вынужденные колебания применяются в различных установках, например в вибромолоте

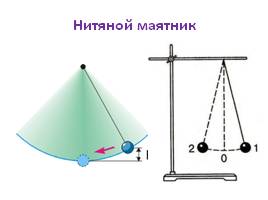
 Колебания являются очень распространенным видом движения. Это покачивание веток деревьев на ветру, качание маятника в настенных часах, волны на воде. Рассмотрим колебательное движение на примере двух маятников.
Нитяной маятник представляет собой шарик, прикрепленный к тонкой, легкой нити. Если шарик сместить в сторону, и отпустить, то он периодически начнет колебаться.
Пружинный маятник представляет собой груз, способный колебаться под действием силы упругости пружины.

Нитяной маятник

Пружинный маятник
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению: F (t) = ma (t) = –m ω2 x (t).
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kx. Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими. Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.

Частота ω0 называется собственной частотой колебательной системы. Период T гармонических колебаний груза на пружине равен

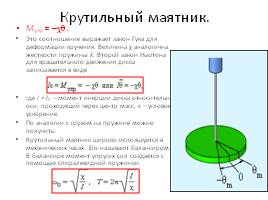
Крутильный маятник.
Mупр = –χθ. Это соотношение выражает закон Гука для деформации кручения. Величина χ аналогична жесткости пружины k. Второй закон Ньютона для вращательного движения диска записывается в виде где I = IC – момент инерции диска относительно оси, проходящий через центр масс, ε – угловое ускорение. По аналогии с грузом на пружине можно получить: Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.

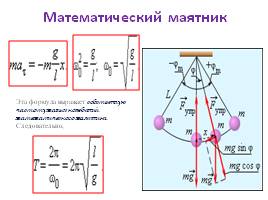
Математический маятник
Эта формула выражает собственную частоту малых колебаний математического маятника. Следовательно,

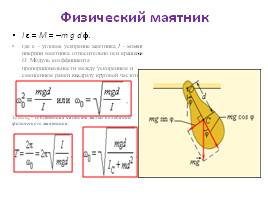
Физический маятник
I ε = M = –m g dφ. где ε – угловое ускорение маятника, I – момент инерции маятника относительно оси вращения O. Модуль коэффициента пропорциональности между ускорением и смещением равен квадрату круговой частоты:
Здесь ω0 – собственная частота малых колебаний физического маятника.