Презентация - Арифметические действия над многочленами (7 класс)

Арифметические действия над многочленами

Многочлен
Что такое многочлен?
Это сумма одночленов
Одночлен
Что такое одночлен?
Произведение числовых и буквенных множителей

Диковинные названия
Как можно по- другому назвать многочлен?
Многочлен -Полином
Как можно назвать одночлен?
Одночлен – МОНОМ
Как можно назвать двучлен?
Двучлен -Бином
Как по другому можно назвать трехчлен?
Трехчлен – Трином
Как называется данный многочлен, учитывая его степень?
Однородный многочлен
Как называется многочлен такого вида?
Многочлен с одной переменной

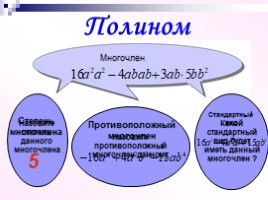
Полином
Многочлен
Степень многочлена
5
Противоположный многочлен
Стандартный вид
Назовите степень данного многочлена
Какой стандартный вид будет иметь данный многочлен ?
Назовите противоположный многочлен данному

Диофант
Древняя Греция. Ученый – математик. III в. до н.э.
В книге «Арифметика» - зачатки буквенной символики и спец обозначения степеней.
Встречаются утверждения о тождественных преобразования многочленов, применение формул и правил.

Проверь правильность решения
(7α5b2c)(-3αb4c)= 21α6b6c2 23α + 19b–12α +11b–9=11α +30b–9 (7m2–4mn–n2)–(2m2–mn+n2)=5m–3mn 5x2y(4xy + 3y2) = 20x3y2 + 15x2y3 (12n3k3 – 15n2k4 ) : (3nk) = 4n2k2–5nk3 (2m – b)(4m2+2mb+b2)=8m3–4m2b+2mb2

Математик (1707 – 1783гг.) Родился 15 апреля 1707 года В швейцарском городе Базеле В семье священника.
Как зовут математика
В 16 лет присвоена ученая степень магистра искусств

Учился на дому у Иоганна Бернулли и дружил с его сыновьями Николаем и Даниилом (также известные ученые математики)
Как зовут математика

20 лет приглашен в Петербургскую Академию Соратник Ломоносова
1727 год
Как зовут математика

Попадает круг выдающихся ученых математиков , физиков, астрономов
Как зовут математика

Создание трудов
Создал более 800 трудов, которые заняли 27 томов Среди них первые учебники, прообразы – современных по решению уравнений Был консультантом и экспертом по разным вопросам науки и техники

Внес огромный вклад в алгебру и теорию чисел, где его работы известны под названием формулы и решение уравнений.
Создание трудов
Известен был в научном мире больше как физик, который построил точную теорию движения луны с учетом притяжения не только Земли, но и Солнца.
Последние 17 лет он слепой продолжал работать и диктовал свои труды ученикам Умер в России…..

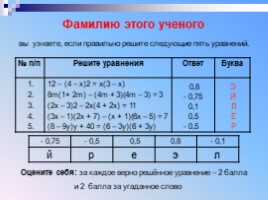
Фамилию этого ученого вы узнаете, если правильно решите следующие пять уравнений.
№ п/п Решите уравнения Ответ Буква
1. 2. 3. 4. 5. 12 – (4 – х)2 = х(3 – х) 8m(1+ 2m) – (4m + 3)(4m – 3) = 3 (2х – 3)2 – 2х(4 + 2х) = 11 (3х – 1)(2х + 7) – (х + 1)(6х – 5) = 7 (8 – 9у)у + 40 = (6 – 3у)(6 + 3у)
- 0,75 - 0,5 0,5 0,8 - 0,1
й р е э л
Оцените себя: за каждое верно решённое уравнение – 2 балла и 2 балла за угаданное слово
0,8 - 0,75 0,1 0,5 - 0,5
Э Й Л Е Р

В клетке сидели фазаны и кролики. У них всего 15 голов и 42 лапки. Сколько кроликов и сколько фазанов было в клетке?
Очень не простая ситуация

Решение задачи:
или
Пусть х – фазанов было, а кроликов – (15 – х), Тогда у фазанов 2х лап, у кроликов – 4(15 – х) лап. По условию задачи было всего 42 лапы, составим уравнение: 2х + 4(15 – х) = 42, 2х +60 – 4х = 42, - 2х = - 18, х = 9 – фазанов. 15 – 9 = 6 – кроликов. Ответ: 6 – кроликов, 9 – фазанов.
Пусть х – кроликов было, а фазанов – (15 – х), Тогда у кроликов 4х лап, у фазанов – 2(15 – х) лап. По условию задачи было всего 42 лапы, составим уравнение: 4х + 2(15 – х) = 42, 4х +30 – 2х = 42, 2х = 12, х = 6 – кроликов. 15 – 6 = 9 – фазанов. Ответ: 6 – кроликов, 9 – фазанов.

Оцените себя:
правильно составлено условие задачи – 2 балла; правильно составлено уравнение – 1 балл; правильно решено уравнение – 2 балла; выполнено следующее действие после уравнения – 1 балл.

Задание на дом:
на уровень «3» - Проверь себя! Стр. 81 на «4 – 5» № 310, 311, 313

Подведение итогов

Благодарю вас за урок!