Презентация - Поверхности второго порядка

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА Определение поверхности второго порядка Цилиндрические поверхности Сфера Трехосный эллипсоид Эллиптический параболоид Однополостный гиперболоид Двуполостный гиперболоид Конус второго порядка Гиперболический параболоид

Определение поверхности второго порядка Поверхность, определяемая уравнением где A,B, H - действительные числа, причем старшие коэффициенты A, B, F не равны нулю одновременно, называется поверхностью второго порядка.

ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ Определение цилиндрической поверхности Уравнение цилиндрической поверхности Эллиптический цилиндр Гиперболический цилиндр Параболический цилиндр

Определение цилиндрической поверхности Поверхность, образованная всеми прямыми, проходящими параллельно данной прямой через точки линии , называется цилиндрической поверхностью При этом линия называется направляющей , а прямые, проходящие через точки кривой параллельно прямой , называется ее образующими. L

Уравнение цилиндрической поверхности, с образующими параллельными оси OZ Пусть на плоскости дана своим уравнением некоторая линия . Проведем через каждую точку кривой прямую параллельно оси . Тогда получим цилиндрическую поверхность с образующими, параллельными этой оси. Уравнение - уравнение этой поверхности. 0 z x M N L y

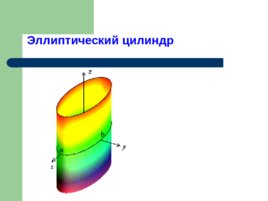
Эллиптический цилиндр

Гиперболический цилиндр

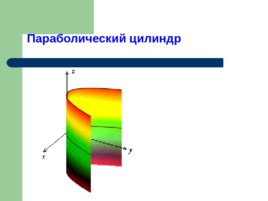
Параболический цилиндр

Эллиптический цилиндр, с образующими, параллельными оси OY Уравнение определяет эллиптический цилиндр с образующими, параллельными оси

Гиперболический цилиндр, с образующими, параллельными оси OX уравнение определяет гиперболический цилиндр с образующими, параллельными оси .

Сфера Множество точек пространства , равноудаленных от одной фиксированной ее точки , называется сферой . Её уравнение имеет вид , где точка - центр сферы, - её радиус

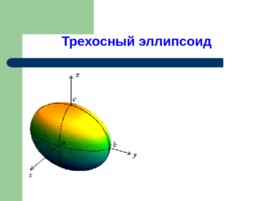
Трехосный эллипсоид

Рассмотрим вначале линии пересечения этой поверхности с горизонтальными плоскостями , где . В сечении, в общем случае, образуется кривая, определяемая уравнениями Сечение эллипсоида плоскостями z h

Сечение эллипсоида плоскостями z h , при Ih I c Горизонтальные плоскости , где , не пересекают данной поверхности (в сечении образуются мнимые кривые).

Сечение эллипсоида плоскостями z h, при Ih I c Рассмотрим сечение Горизонтальной плоскостью , где , то Следовательно, в сечениях и получим точки и .

Сечение эллипсоида плоскостью z h, при Ih I Если , то . Тогда в сечении горизонтальной плоскостью , где , получим линию где Уравнение на плоскости определяет эллипс с полуосями и

Сечение эллипсоида плоскостями x h и y h Так как уравнение обладает симметрией относительно переменных и , то в сечениях вертикальными плоскостями где и , где , так же образуются эллипсы или точки.

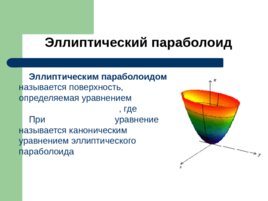
Эллиптический параболоид Эллиптическим параболоидом называется поверхность, определяемая уравнением , где При уравнение называется каноническим уравнением эллиптического параболоида

Сечение эллиптического параболоида плоскостями z h Рассмотрим сечения поверхности горизонтальными плоскостями , где . В сечении, в общем случае, получим линию:

Сечение эллиптического параболоида плоскостями z h, при h Так как по условию и , то при любых значениях и . Следовательно, при горизонтальные плоскости не пересекают поверхность.

Сечение эллиптического параболоида плоскостями z h , при h 0 и h 0 При , то есть на плоскости , получим точку . При на плоскости получим линию , где ( ) Уравнение ( ) на плоскости определяет эллипс с полуосями и

Сечение эллиптического параболоида плоскостями y h Рассмотрим сечение вертикальной плоскостью , где . В сечении получим линию: Уравнение на плоскости определяет параболу с осью симметрии , параметром и вершиной, находящейся в точке .

Параболоид вращения Если в уравнении , то в сечениях горизонтальными плоскостями образуются окружности. Следовательно, уравнение определяет параболоид вращения с осью симметрии .

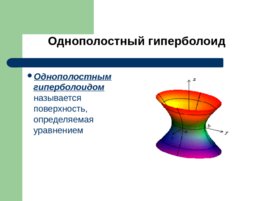
Однополостный гиперболоид Однополостным гиперболоидом называется поверхность, определяемая уравнением

Сечение однополостного гиперболоида плоскостями z h В сечениях горизонтальными плоскостями , где , получим линии где . Таким образом, в сечениях плоскостями образуются эллипсы с полуосями и

Сечение однополостного гиперболоида плоскостями y h, при Ih I Пусть , где . В сечениях образуются линии Если , то Тогда на плоскости , получим гиперболу , где с действительной полуосью и мнимой .

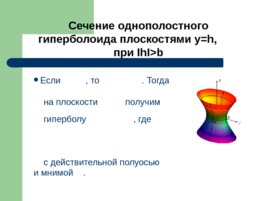
Сечение однополостного гиперболоида плоскостями y h , при Ih I b Если , то . Тогда на плоскости получим гиперболу , где с действительной полуосью и мнимой .

Сечение однополостного гиперболоида плоскостями y h , при Ih I b Если , то . Тогда из уравнения получим пару пересекающихся прямых.

Сечение однополостного гиперболоида плоскостями x h В сечениях вертикальными плоскостями , где , образуются так же, как и в сечениях , либо гиперболы, либо пара пересекающихся прямых (исследовать самостоятельно).

Двуполостный гиперболоид Двуполостным гиперболоидом называется поверхность, заданная уравнением

Сечение двуполостного гиперболоида плоскостями z h , при Ih I Рассмотрим сечения горизонтальными плоскостями , где . В сечениях образуются линии Так как при любых значениях и , то при первое уравнение не выполняется ни при каких и . Следовательно, плоскости , где , не пересекают данную поверхность

Сечение двуполостного гиперболоида плоскостями z h , при Ih I c Если , то Следовательно, в сечениях плоскостями и образуется пара точек с координатами и .

Сечение двуполостного гиперболоида плоскостями z h , при Ih I c Если , то . Следовательно, первое уравнение из можно записать в форме где Уравнение является уравнением эллипса с полуосями и .

Сечение двуполостного гиперболоида плоскостями y h Пусть , где . Тогда в сечениях, получим линии Следовательно, на плоскости при любых значениях образуется гипербола где с действительной полуосью и мнимой полуосью , ориентированная вдоль оси

Сечение двуполостного гиперболоида плоскостями x h В сечениях вертикальными плоскостями , где , так же образуются гиперболы, ориентированные вдоль оси (исследовать самостоятельно).

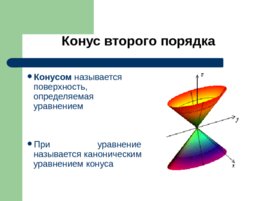
Конус второго порядка Конусом называется поверхность, определяемая уравнением При уравнение называется каноническим уравнением конуса

Конусы второго порядка с осями симметрии OX и OY Конусы с осями симметрии и соответственно задаются уравнениями

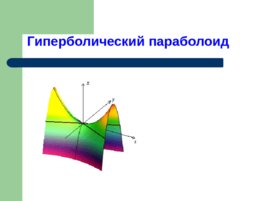
Гиперболический параболоид